Effect of dielectrics in capacitors

Effect of dielectrics in capacitors

In earlier discussions, we assumed that the space between the parallel plates of a capacitor is either empty or filled with air. Suppose dielectrics like mica, glass or paper are introduced between the plates, then the capacitance of the capacitor is altered. The dielectric can be inserted into the plates in two different ways. (i) when the capacitor is disconnected from the battery. (ii) when the capacitor is connected to the battery.

(i) when the capacitor is disconnected from the battery

Consider a capacitor with two parallel plates each of cross-sectional area A and are separated by a distance d. The capacitor is charged by a battery of voltage V₀ and the charge stored is Q₀. The capacitance of the capacitor without the dielectric is

The battery is then disconnected from the capacitor and the dielectric is inserted between the plates. This is shown in Figure 1.58.

The introduction of dielectric between the plates will decrease the electric field. Experimentally it is found that the modified electric field is given by

Here E_o is the electric field inside the capacitors when there is no dielectric and ε_r is the relative permeability of the dielectric or simply known as the dielectric constant. Since ε_r > 1, the electric field E < E_o.

As a result, the electrostatic potential difference between the plates (V = Ed) is also reduced. But at the same time, the charge Q_o will remain constant once the battery is disconnected.

Hence the new potential difference is

We know that capacitance is inversely proportional to the potential difference. Therefore as V decreases, C increases.

Thus new capacitance in the presence of a dielectric is

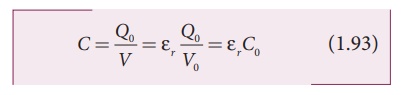
Since ε_r > 1, we have C > C_o. Thus insertion of the dielectric constant ε_r increases the capacitance.

Using equation (1.84),

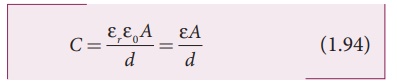
where ε = ε_r ε_o is the permittivity of the dielectric medium.

The energy stored in the capacitor before the insertion of a dielectric is given by

After the dielectric is inserted, the charge Q₀ remains constant but the capacitance is increased. As a result, the stored energy is decreased.

Since ε_r > 1 we get U < U_o. There is a decrease in energy because,when the dielectric is inserted, the capacitor spends some energy in pulling the dielectric inside.

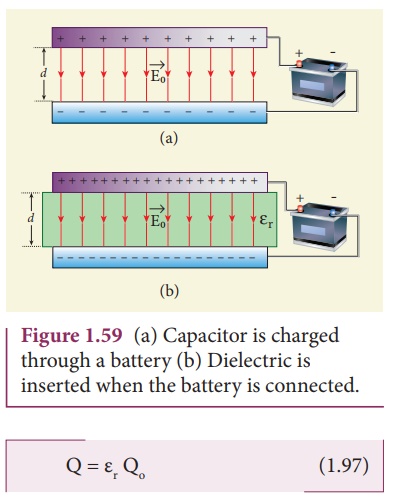
(ii) When the battery remains connected to the capacitor

Let us now consider what happens when the battery of voltage V₀ remains connected to the capacitor when the dielectric is inserted into the capacitor. This is shown in Figure1.59.

The potential difference V₀ across the plates remains constant. But it is found experimentally (first shown by Faraday) that when dielectric is inserted, the charge stored in the capacitor is increased by a factor ε_r.

Due to this increased charge, the capacitance is also increased. The new capacitance is

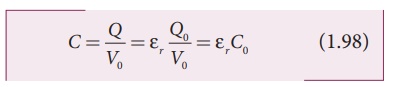
However the reason for the increase in capacitance in this case when the battery remains connected is different from the case when the battery is disconnected before introducing the dielectric.

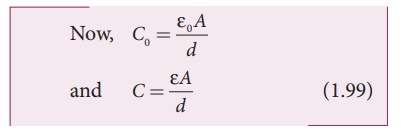
The energy stored in the capacitor before the insertion of a dielectric is given by

Note that here we have not used the expression 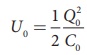 because here, both charge and capacitance are changed, whereas in equation (1.100), V_o remains constant.

After the dielectric is inserted, the capacitance is increased; hence the stored energy is also increased.

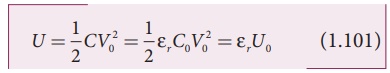
Since ε_r > 1 we have U > U_o.

It may be noted here that since voltage between the capacitor V₀ is constant, the electric field between the plates also remains constant.

The energy density is given by

where ε is the permittivity of the given dielectric material.

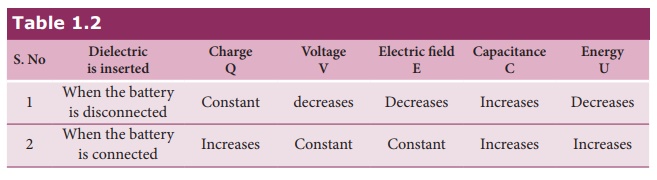
The results of the above discussions are summarised in the following Table 1.2

EXAMPLE 1.21

A parallel plate capacitor filled with mica having ε_r = 5 is connected to a 10 V battery. The area of the parallel plate is 6 m2 and separation distance is 6 mm.

(a) Find the capacitance and stored charge.

(b) After the capacitor is fully charged, the battery is disconnected and the dielectric is removed carefully.

Calculate the new values of capacitance, stored energy and charge.

Solution

(a) The capacitance of the capacitor in the presence of dielectric is

(b) After the removal of the dielectric, since the battery is already disconnected the total charge will not change. But the potential difference between the plates increases. As a result, the capacitance is decreased.

New capacitance is

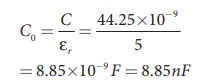
The stored charge remains same and 442.5 nC. Hence newly stored energy is

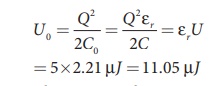
The increased energy is

∆U = 11.05µ J −2.21 µ J = 8.84 µ J

When the dielectric is removed, it experiences an inward pulling force due to the plates. To remove the dielectric, an external agency has to do work on the dielectric which is stored as additional energy. This is the source for the extra energy 8.84 µJ.