Electric field due to a dipole

Electric field due to a dipole

Case (i) Electric field due to an electric dipole at points on the axial line 

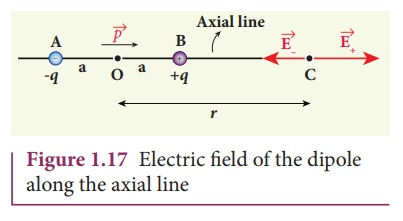
Consider an electric dipole placed on the x-axis as shown in Figure 1.17. A point C is located at a distance of r from the midpoint O of the dipole along the axial line.

The electric field at a point C due to +q is

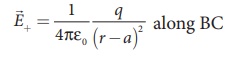
Since the electric dipole moment vector  is from –q to +q and is directed along BC, the above equation is rewritten as

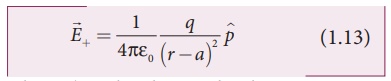
where p ^ is the electric dipole moment unit vector from –q to +q.

The electric field at a point C due to –q is

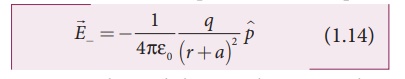
Since +q is located closer to the point C than –q, ₊ is stronger than _- . Therefore, the length of the ₊ vector is drawn larger than that of _- vector.

The total electric field at point C is calculated using the superposition principle of the electric field.

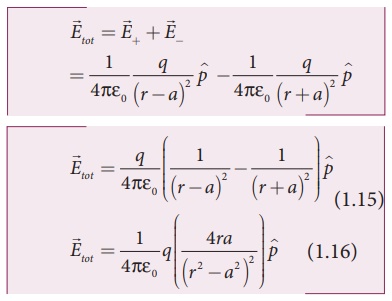
Note that the total electric field is along ₊ , since +q is closer to C than –q.

The direction of _tot  is shown in Figure 1.18.

If the point C is very far away from the dipole then (r >> a). Under this limit the term ( r² − a² )² ≈ r⁴ . Substituting this into equation (1.16), we get

If the point C is chosen on the left side of the dipole, the total electric field is still in the direction of . We infer this result by examining the electric field lines of the dipole shown in Figure 1.16(b).

Case (ii) Electric field due to an electric dipole at a point on the equatorial plane

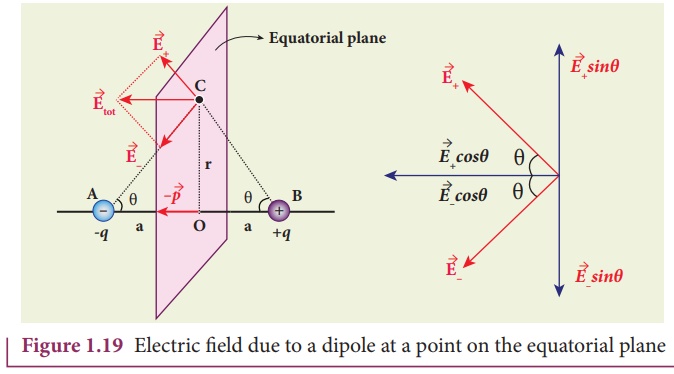
Consider a point C at a distance r from the midpoint O of the dipole on the equatorial plane as shown in Figure 1.19.

Since the point C is equi-distant from +q and –q, the magnitude of the electric fields of +q and –q are the same. The direction of ₊ is along BC and the direction of _- is along CA. ₊ and _- are resolved into two components; one component parallel to the dipole axis and the other perpendicular to it. The perpendicular components | ₊| sinθ and | _-| sinθ are oppositely directed and cancel each other. The magnitude of the total electric field at point C is the sum of the parallel components of ₊ and _- and its direction is along -^p as shown in the Figure 1.19.

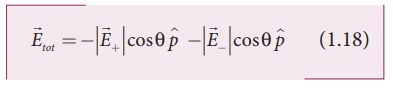
The magnitudes ₊ and _- are the same and are given by

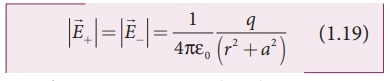
By substituting equation (1.19) into equation (1.18), we get

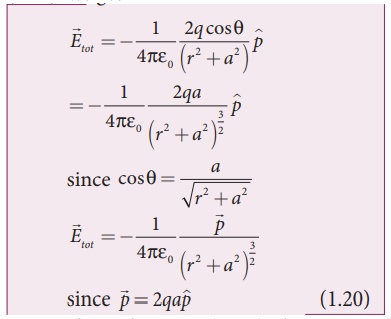
At very large distances (r>>a), the equation (1.20) becomes

Important inferences

(i) From equations (1.17) and (1.21), it is inferred that for very large distances, the magnitude of the electric field at points on the dipole axis is twice the magnitude of the electric field at points on the equatorial plane. The direction of the electric field at points on the dipole axis is directed along the direction of dipole moment vector  but at points on the equatorial plane it is directed opposite to the dipole moment vector, that is along -.

(ii) At very large distances, the electric field due to a dipole varies as 1/r³ . Note that for a point charge, the electric field varies as 1/r² . This implies that the electric field due to a dipole at very large distances goes to zero faster than the electric field due to a point charge. The reason for this behavior is that at very large distance, the two charges appear to be close to each other and neutralize each other.

(iii) The equations (1.17) and (1.21) are valid only at very large distances (r>>a). Suppose the distance 2a approaches zero and q approaches infinity such that the product of 2aq = p is finite, then the dipole is called a point dipole. For such point dipoles, equations (1.17) and (1.21) are exact and hold true for any r.