Electric potential due to a point charge

Electric potential due to a point charge

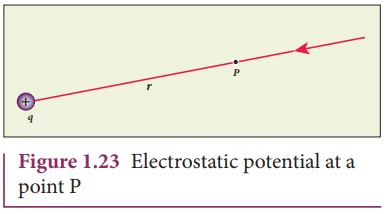
Consider a positive charge q kept fixed at the origin. Let P be a point at distance r from the charge q. This is shown in Figure 1.23.

The electric potential at the point P is

Electric field due to positive point charge q is

Hence the electric potential due to a point charge q at a distance r is

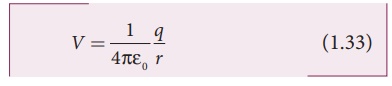
Important points

(i) If the source charge q is positive, V > 0. If q is negative, then V is negative and equal to

(ii) The description of motion of objects using the concept of potential or potential energy is simpler than that using the concept of field.

(iii) From expression (1.33), it is clear that the potential due to positive charge decreases as the distance increases, but for a negative charge the potential increases as the distance is increased. At infinity (r = ∞) electrostatic potential is zero (V = 0).

In the case of gravitational force, mass moves from a point of higher gravitational potential to a point of lower gravitational potential. Similarly a positive charge moves from a point of higher electrostatic potential to lower electrostatic potential. However a negative charge moves from lower electrostatic potential to higher electrostatic potential. This comparison is shown in Figure 1.24.

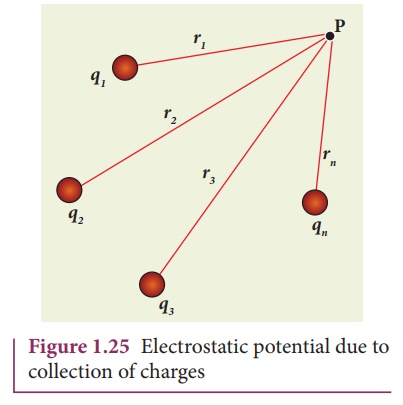
(iv) The electric potential at a point P due to a collection of charges q₁,q_2,q₃…..q_n is equal to sum of the electric potentials due to individual charges.

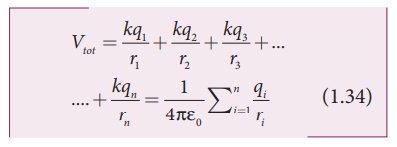
where  r₁,r₂,r₃…….r_n are the distances of q₁, q₂, q₃ ….. q_n respectively      from P (Figure 1.25).

EXAMPLE 1.12

(a) Calculate the electric potential at points P and Q as shown in the figure below.

(b) Suppose the charge +9µC is replaced by -9µC find the electrostatic potentials at points P and Q

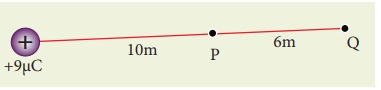
( c )  Calculate the work done to bring a test charge +2µC from infinity to the point P. Assume the charge +9µC is held fixed at origin and +2µC is brought from infinity to P.

Solution

(a) Electric potential at point P is given by

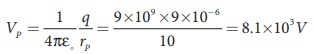
Electric potential at point Q is given by

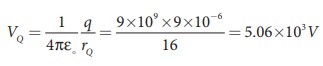
Note that the electric potential at point Q is less than the electric potential at point P. If we put a positive charge at P, it moves from P to Q. However if we place a negative charge at P it will move towards the charge +9µC.

The potential difference between the points P and Q is given by

∆V = V_P −V_Q = +3 .04 ×10³V

(b) Suppose we replace the charge +9 µC by -9 µC, then the corresponding potentials at the points P and Q are,

V_P = −8 . 1×10³ V , V_Q =− 5.06 ×10³V

Note that in this case electric potential at the point Q is higher than at point P.

The potential difference or voltage between the points P and Q is given by

∆V = V_P −V_Q = −3 .04 ×10³V

(c) The electric potential V at a point P due to some charge is defined as the work done by an external force to bring a unit positive charge from infinity to P. So to bring the q amount of charge from infinity to the point P, work done is given as follows.

W = qV

W_Q = 2 ×10− ⁶ × 5. 06 ×10³ J = 10 .12 ×10^−3 J.

EXAMPLE 1.13

Consider a point charge +q placed at the origin and another point charge -2q placed at a distance of 9 m from the charge +q. Determine the point between the two charges at which electric potential is zero.

Solution

According to the superposition principle, the total electric potential at a point is equal to the sum of the potentials due to each charge at that point.

Consider the point at which the total potential zero is located at a distance x from the charge +q as shown in the figure.