Conductors at electrostatic equilibrium

ELECTROSTATICS OF CONDUCTORS AND DIELECTRICS

Conductors at electrostatic equilibrium

An electrical conductor has a large number of mobile charges which are free to move in the material. In a metallic conductor, these mobile charges are free electrons which are not bound to any atom and therefore are free to move on the surface of the conductor. When there is no external electric field, the free electrons are in continuous random motion in all directions. As a result, there is no net motion of electrons along any particular direction which implies that the conductor is in electrostatic equilibrium. Thus at electrostatic equilibrium, there is no net current in the conductor. A conductor at electrostatic equilibrium has the following properties.

(i) The electric field is zero everywhere inside the conductor. This is true regardless of whether the conductor is solid or hollow.

This is an experimental fact. Suppose the electric field is not zero inside the metal, then there will be a force on the mobile charge carriers due to this electric field. As a result, there will be a net motion of the mobile charges, which contradicts the conductors being in electrostatic equilibrium. Thus the electric field is zero everywhere inside the conductor. We can also understand this fact by applying an external uniform electric field on the conductor. This is shown in Figure 1.44.

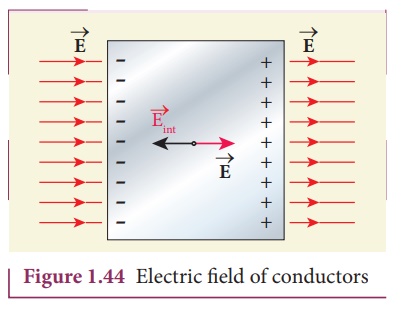
Before applying the external electric field, the free electrons in the conductor are uniformly distributed in the conductor. When an electric field is applied, the free electrons accelerate to the left causing the left plate to be negatively charged and the right plate to be positively charged as shown in Figure 1.44.

Due to this realignment of free electrons, there will be an internal electric field created inside the conductor which increases until it nullifies the external electric field. Once the external electric field is nullified the conductor is said to be in electrostatic equilibrium. The time taken by a conductor to reach electrostatic equilibrium is in the order of 10-16 s, which can be taken as almost instantaneous.

(ii) There is no net charge inside the conductors. 

There is no net charge inside the conductors. The charges must reside only on the surface of the conductors. We can prove this property using Gauss law. Consider an arbitrarily shaped conductor as shown in Figure 1.45.

A Gaussian surface is drawn inside the conductor such that it is very close to the surface of the conductor. Since the electric field is zero everywhere inside the conductor, the net electric flux is also zero over this Gaussian surface. 

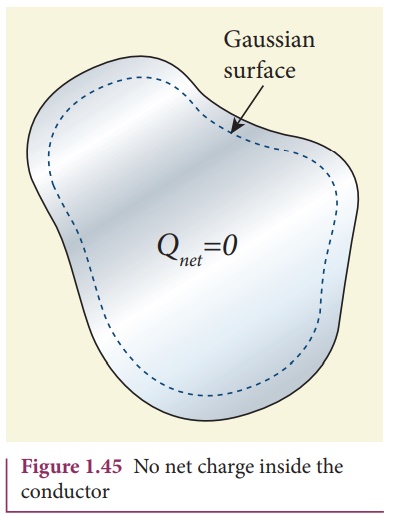
From Gauss’s law, this implies that there is no net charge inside the conductor. Even if some charge is introduced inside the conductor, it immediately reaches the surface of the conductor.

(iii) The electric field outside the conductor is perpendicular to the surface of the conductor and has a magnitude of σ /ε₀ where σ is the surface charge density at that point.

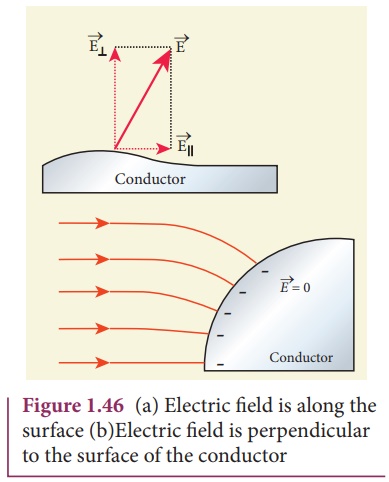
If the electric field has components parallel to the surface of the conductor, then free electrons on the surface of the conductor would experience acceleration (Figure 1.46(a)). This means that the conductor is not in equilibrium. Therefore at electrostatic equilibrium, the electric field must be perpendicular to the surface of the conductor. This is shown in Figure 1.46 (b).

We now prove that the electric field has magnitude σ /ε₀ just outside the conductor’s ε surface. Consider a small cylindrical Gaussian surface, as shown in the Figure 1.47. One half of this cylinder is embedded inside the conductor.

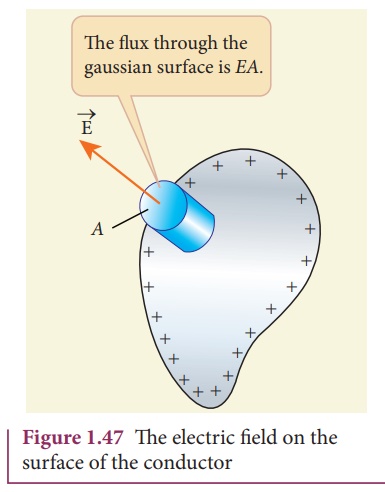
Since electric field is normal to the surface of the conductor, the curved part of the cylinder has zero electric flux. Also inside the conductor, the electric field is zero. Hence the bottom flat part of the Gaussian surface has no electric flux.

Therefore the top flat surface alone contributes to the electric flux. The electric field is parallel to the area vector and the total charge inside the surface is σA. By applying Gaus’s law,

Here n ^  represents the unit vector outward normal to the surface of the conductor. Suppose σ < 0, then electric field points inward perpendicular to the surface.

(iv) The electrostatic potential has the same value on the surface and inside of the conductor.

We know that the conductor has no parallel electric component on the surface which means that charges can be moved on the surface without doing any work. This is possible only if the electrostatic potential is constant at all points on the surface and there is no potential difference between any two points on the surface.

Since the electric field is zero inside the conductor, the potential is the same as the surface of the conductor. Thus at electrostatic equilibrium, the conductor is always at equipotential.