Chapter: 12th Physics : Electrostatics
Capacitors and Capacitance: Solved Example Problems
Capacitors: Solved Example Problems
Example 1.20
A parallel plate capacitor has square plates of side 5 cm and separated by a distance of 1 mm. (a) Calculate the capacitance of this capacitor. (b) If a 10 V battery is connected to the capacitor, what is the charge stored in any one of the plates? (The value of εo = 8.85 x 10-12 Nm2 C-2)
Solution
(a) The capacitance of the capacitor is
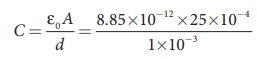
= 221.2 ×10−13 F
C = 22 . 12 ×10−12 F = 22 .12 pF
(b) The charge stored in any one of the plates is Q = CV, Then
= 22 . 12 ×10−12 ×10 = 221.2 ×10−12 C = 221.2 pC
Capacitance of a parallel plate capacitor: Solved Example Problems
Example 1.20
A parallel plate capacitor has square plates of side 5 cm and separated by a distance of 1 mm. (a) Calculate the capacitance of this capacitor. (b) If a 10 V battery is connected to the capacitor, what is the charge stored in any one of the plates? (The value of εo = 8.85 x 10-12 Nm2 C-2)
Solution
(a) The capacitance of the capacitor is
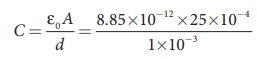
= 221.2 ×10−13 F
C = 22 . 12 ×10−12 F = 22 .12 pF
(b) The charge stored in any one of the plates is Q = CV, Then
= 22 . 12 ×10−12 ×10 = 221.2 ×10−12 C = 221.2 pC
Effect of dielectrics in capacitors: Solved Example Problems
EXAMPLE 1.21
A parallel plate capacitor filled with mica having εr = 5 is connected to a 10 V battery. The area of the parallel plate is 6 m2 and separation distance is 6 mm.
(a) Find the capacitance and stored charge.
(b) After the capacitor is fully charged, the battery is disconnected and the dielectric is removed carefully.
Calculate the new values of capacitance, stored energy and charge.
Solution
(a) The capacitance of the capacitor in the presence of dielectric is

(b) After the removal of the dielectric, since the battery is already disconnected the total charge will not change. But the potential difference between the plates increases. As a result, the capacitance is decreased.
New capacitance is
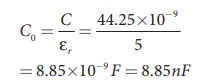
The stored charge remains same and 442.5 nC. Hence newly stored energy is
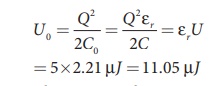
The increased energy is
∆U = 11.05µ J −2.21 µ J = 8.84 µ J
When the dielectric is removed, it experiences an inward pulling force due to the plates. To remove the dielectric, an external agency has to do work on the dielectric which is stored as additional energy. This is the source for the extra energy 8.84 µJ.
Capacitor in series and parallel: Solved Example Problems
EXAMPLE 1.22
Find the equivalent capacitance between P and Q for the configuration shown below in the figure (a).
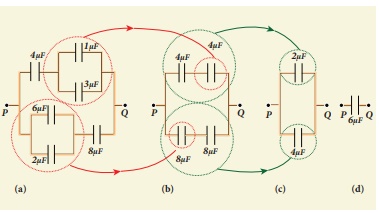
Solution
The capacitors 1 µF and 3µF are connected in parallel and 6µF and 2 µF are also separately connected in parallel. So these parallel combinations reduced to equivalent single capacitances in their respective positions, as shown in the figure (b).
Ceq = 1µF + 3µF = 4µF
Ceq = 6µF + 2µF = 8µF
From the figure (b), we infer that the two 4 µF capacitors are connected in series and the two 8 µF capacitors are connected in series. By using formula for the series, we can reduce to their equivalent capacitances as shown in figure (c).

From the figure (c), we infer that 2µF and 4µF are connected in parallel. So the equivalent capacitance is given in the figure (d).
Ceq = 2µF + 4µF = 6µF
Thus the combination of capacitances in figure (a) can be replaced by a single capacitance 6 µF.
Related Topics