Electric field due to the system of point charges

Electric field due to the system of point charges

Suppose a number of point charges are distributed in space. To find the electric field at some point P due to this collection of point charges, superposition principle is used. The electric field at an arbitrary point due to a collection of point charges is simply equal to the vector sum of the electric fields created by the individual point charges. This is called superposition of electric fields.

Consider a collection of point charges q₁ , q₂ ,q ₃ ..........q_n located at various points in space. The total electric field at some point P due to all these n charges is given by

Here r_1P , r_2P ,r_3P   ..........r_nP     are the distance of the the charges q₁ , q₂ ,q₃ ..........       q_n from the point respectively. Also ^r_1P , ^r_2P , ^r_3P ..........r ^_nP are the corresponding unit vectors directed from q₁, q₂ ,q₃ ..........q_n to P.

Equation (1.7) can be re-written as,

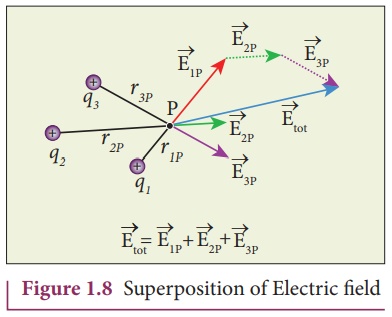
For example in Figure 1.8, the resultant electric field due to three point charges q₁ ,q₂ ,q₃ at point P is shown.

Note that the relative lengths of the electric field vectors for the charges depend on relative distances of the charges to the point P.

EXAMPLE 1.7

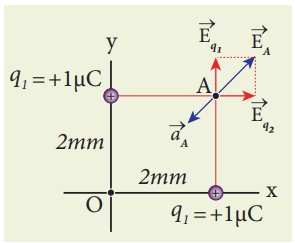
Consider the charge configuration as shown in the figure. Calculate the electric field at point A. If an electron is placed at points A, what is the acceleration experienced by this electron? (mass of the electron = 9.1 × 10^-31 kg and charge of electron = −1.6 × 10^-19 C)

Solution

By using superposition principle, the net electric field at point A is

where r_1A and r_2A are the distances of point A from the two charges respectively.

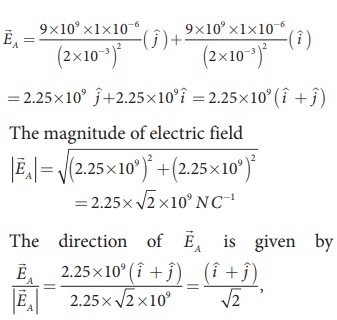
which is the unit vector along OA as shown in the figure.

The acceleration experienced by an electron placed at point A is 

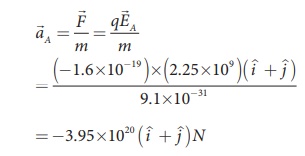
The electron is accelerated in a direction exactly opposite to A.