Distribution of Charges in a Conductor and Action at Points: Solved Example Problems

Distribution of charges in a conductor: Solved Example Problems

EXAMPLE 1.23

Two conducting spheres of radius r1 = 8 cm and r2 = 2 cm are separated by a distance much larger than 8 cm and are connected by a thin conducting wire as shown in the figure. A total charge of Q = +100 nC is placed on one of the spheres. After a fraction of a second, the charge Q is redistributed and both the spheres attain electrostatic equilibrium.

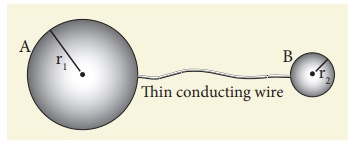
(a) Calculate the charge and surface charge density on each sphere.

(b) Calculate the potential at the surface of each sphere.

Solution

(a) The electrostatic potential on the surface of the sphere A is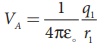 

The electrostatic potential on the surface of the sphere A is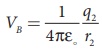 

Since VA = VB. We have

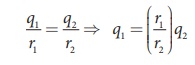
But from the conservation of total charge, Q  = q1 + q2, we get q1 = Q – q2. By substituting this in the above equation,

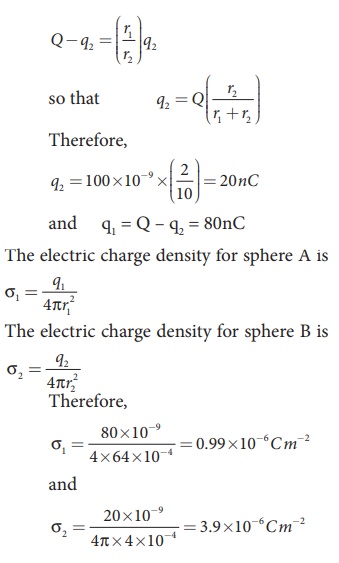
Note that the surface charge density is greater on the smaller sphere compared to the larger sphere (σ2 â‰ˆ 4σ1) which confirms the result σ1 / σ1= r2 / r2.

The potential on both spheres is the same. So we can calculate the potential on any one of the spheres.

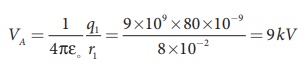
Van de Graaff Generator: Solved Example Problems

EXAMPLE 1.24

Dielectric strength of air is 3 × 106 V m-1. Suppose the radius of a hollow sphere in the Van de Graff generator is R = 0.5 m, calculate the maximum potential difference created by this Van de Graaff generator.

The electric field on the surface of the sphere (by Gauss law) is given by

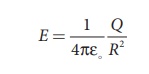
The potential on the surface of the hollow metallic sphere is given by

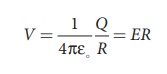
with Vmax = EmaxR

Here Emax = 3 ×106 V/m . So the maximum potential difference created is given by

Vmax = 3 × 106 Ã— 0.5

= 1.5 × 106 V (or) 1.5 million volt