Capacitor in series and parallel

Capacitor in series and parallel

(i) Capacitor in series

Consider three capacitors of capacitance C₁, C₂ and C₃ connected in series with a battery of voltage V as shown in the Figure 1.60 (a).

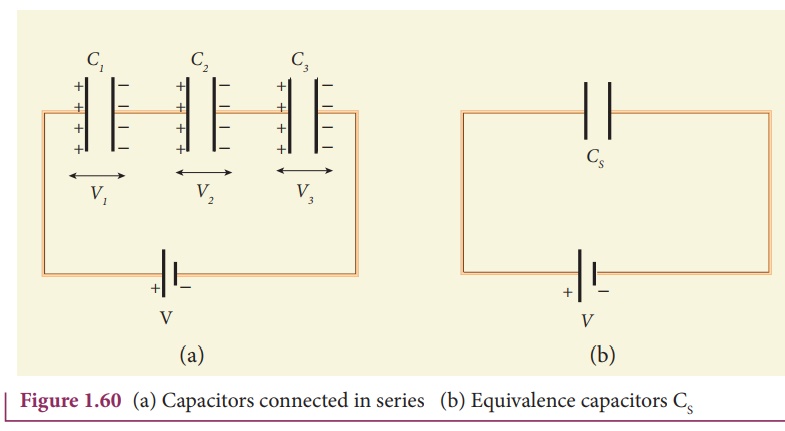
As soon as the battery is connected to the capacitors in series, the electrons of charge â€“Q are transferred from negative terminal to the right plate of C₃ which pushes the electrons of same amount -Q from left plate of C₃ to the right plate of C₂ due to electrostatic induction. Similarly, the left plate of C₂ pushes the charges of –Q to the right plate of C₁ which induces the positive charge +Q on the left plate of C₁. At the same time, electrons of charge –Q are transferred from left plate of C₁ to positive terminal of the battery.

By these processes, each capacitor stores the same amount of charge Q. The capacitances of the capacitors are in general different, so that the voltage across each capacitor is also different and are denoted as V₁, V₂ and V₃ respectively.

The total voltage across each capacitor must be equal to the voltage of the battery.

If three capacitors in series are considered to form an equivalent single capacitor C_s shown in Figure 1.60(b), then we have V=Q/C_s.  Substituting this expression into  equation (1.104), we get

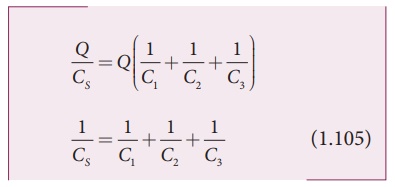
Thus, the inverse of the equivalent capacitance C_S of three capacitors connected in series is equal to the sum of the inverses of each capacitance. This equivalent capacitance C_S is always less than the smallest individual capacitance in the series.

(ii) Capacitance in parallel

Consider three capacitors of capacitance C₁, C₂ and C₃ connected in parallel with a battery of voltage V as shown in Figure 1.61 (a).

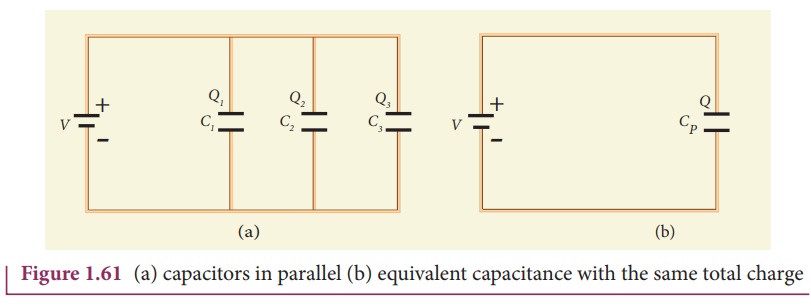
Since corresponding sides of the capacitors are connected to the same positive and negative terminals of the battery, the voltage across each capacitor is equal to the battery’s voltage. Since capacitance of the capacitors is different, the charge stored in each capacitor is not the same. Let the charge stored in the three capacitors be Q₁, Q_2, and Q₃ respectively. According to the law of conservation of total charge, the sum of these three charges is equal to the charge Q transferred by the battery,

If these three capacitors are considered to form a single capacitance C_P which stores the total charge Q as shown in the Figure 1.61(b), then we can write Q = C_PV. Substituting this in equation (1.107), we get

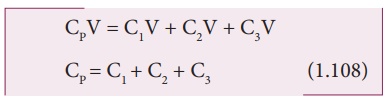
Thus, the equivalent capacitance of capacitors connected in parallel is equal to the sum of the individual capacitances.

The equivalent capacitance C_P in a parallel connection is always greater than the largest individual capacitance. In a parallel connection, it is equivalent as area of each capacitance adds to give more effective area such that total capacitance increases.

EXAMPLE 1.22

Find the equivalent capacitance between P and Q for the configuration shown below in the figure (a).

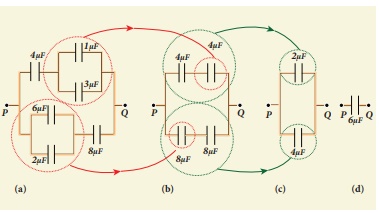
Solution

The capacitors 1 µF and 3µF are connected in parallel and 6µF and 2 µF are also separately connected in parallel. So these parallel combinations reduced to equivalent single capacitances in their respective positions, as shown in the figure (b).

C_eq = 1µF + 3µF = 4µF

C_eq = 6µF + 2µF = 8µF

From the figure (b), we infer that the two 4 µF capacitors are connected in series and the two 8 µF capacitors are connected in series. By using formula for the series, we can reduce to their equivalent capacitances as shown in figure (c).

From the figure (c), we infer that 2µF and 4µF are connected in parallel. So the equivalent capacitance is given in the figure (d).

C_eq = 2µF + 4µF = 6µF

Thus the combination of capacitances in figure (a) can be replaced by a single capacitance 6 µF.