Chapter: 12th Physics : Electrostatics
Electrostatic Potential and Potential Energy: Solved Example Problems
Electric potential due to a point charge
EXAMPLE 1.12
(a) Calculate the electric potential at points P and Q as shown in the figure below.
(b) Suppose the charge +9µC is replaced by -9µC find the electrostatic potentials at points P and Q
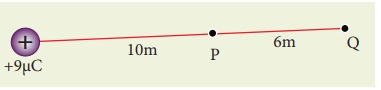
( c ) Calculate the work done to bring a test charge +2µC from infinity to the point P. Assume the charge +9µC is held fixed at origin and +2µC is brought from infinity to P.
Solution
(a) Electric potential at point P is given by
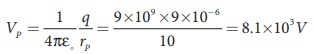
Electric potential at point Q is given by
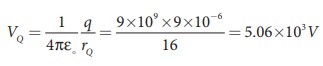
Note that the electric potential at point Q is less than the electric potential at point P. If we put a positive charge at P, it moves from P to Q. However if we place a negative charge at P it will move towards the charge +9µC.
The potential difference between the points P and Q is given by
∆V = VP −VQ = +3 .04 ×103V
(b) Suppose we replace the charge +9 µC by -9 µC, then the corresponding potentials at the points P and Q are,
VP = −8 . 1×103 V , VQ =− 5.06 ×103V
Note that in this case electric potential at the point Q is higher than at point P.
The potential difference or voltage between the points P and Q is given by
∆V = VP −VQ = −3 .04 ×103V
(c) The electric potential V at a point P due to some charge is defined as the work done by an external force to bring a unit positive charge from infinity to P. So to bring the q amount of charge from infinity to the point P, work done is given as follows.
W = qV
WQ = 2 ×10− 6 × 5. 06 ×103 J = 10 .12 ×10−3 J.
EXAMPLE 1.13
Consider a point charge +q placed at the origin and another point charge -2q placed at a distance of 9 m from the charge +q. Determine the point between the two charges at which electric potential is zero.
Solution
According to the superposition principle, the total electric potential at a point is equal to the sum of the potentials due to each charge at that point.
Consider the point at which the total potential zero is located at a distance x from the charge +q as shown in the figure.

Relation between electric field and potential
EXAMPLE 1.14
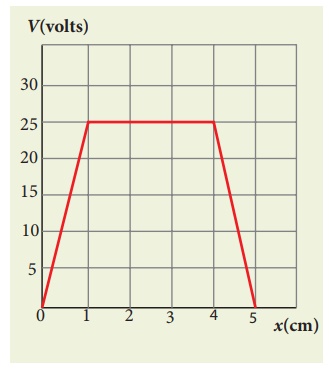
The following figure represents the electric potential as a function of x – coordinate. Plot the corresponding electric field as a function of x.
Solution
In the given problem, since the potential depends only on x, we can use 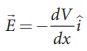 (the other two terms ∂V/∂y and ∂V/∂z are zero)
(the other two terms ∂V/∂y and ∂V/∂z are zero)
From 0 to 1 cm, the slope is constant and so dV/dx = 25V cm−1.
So ![]() = −25V cm−1
= −25V cm−1 ![]()
From 1 to 4 cm, the potential is constant, V = 25 V. It implies that dV/dx = 0. So ![]() = 0
= 0
From 4 to 5 cm, the slope dV/dx = −25V cm−1.
So ![]() = +25V cm−1
= +25V cm−1 ![]()
The plot of electric field for the various points along the x axis is given below.

Electrostatic potential energy for collection of point charges
EXAMPLE 1.15
Four charges are arranged at the corners of the square PQRS of side a as shown in the figure.(a) Find the work required to assemble these charges in the given configuration. (b) Suppose a charge q′ is brought to the center of the square, by keeping the four charges fixed at the corners, how much extra work is required for this?
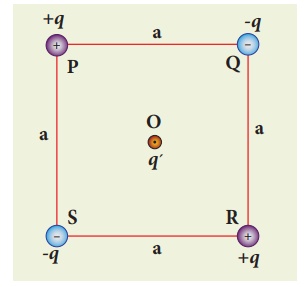
Solution
(a) The work done to arrange the charges in the corners of the square is independent of the way they are arranged. We can follow any order.
(i) First, the charge +q is brought to the corner P. This requires no work since no charge is already present, WP = 0
(ii) Work required to bring the charge –q to the corner Q = (-q) x potential at a point Q due to +q located at a point P.
WQ = −q × 1/4πε . q/ = − 1/4πε . q2/a

(iii) Work required to bring the charge +q to the corner R= q × potential at the point R due to charges at the point P and Q.

(iv) Work required to bring the fourth charge –q at the position S = q × potential at the point S due the all the three charges at the point P, Q and R
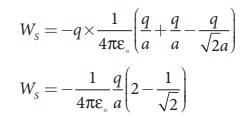
(b) Work required to bring the charge q′ to the center of the square = q′ × potential at the center point O due to all the four charges in the four corners
The potential created by the two +q charges are canceled by the potential created by the -q charges which are located in the opposite corners. Therefore the net electric potential at the center O due to all the charges in the corners is zero.
Hence no work is required to bring any charge to the point O. Physically this implies that if any charge q′ when brought close to O, then it moves to the point O without any external force.
Electrostatic potential energy of a dipole in a uniform electric field
EXAMPLE 1.16
A water molecule has an electric dipole moment of 6.3 × 10-30 Cm. A sample contains 1022 water molecules, with all the dipole moments aligned parallel to the external electric field of magnitude 3 × 105 N C-1. How much work is required to rotate all the water molecules from θ = 0º to 90º?
Solution
When the water molecules are aligned in the direction of the electric field, it has minimum potential energy. The work done to rotate the dipole from θ = 0º to 90º is equal to the potential energy difference between these two configurations.
W= ∆U =U (90º)−U (0º)
From the equation (1.51), we write U = − pE cosθ, Next we calculate the work done to rotate one water molecule from θ = 0º to 90º.
For one water molecule
W = −pE cos 90º + pE cos0º = pE
W = 6 . 3×10− 30 × 3 ×105 = 18 .9×10−25 J
For 1022 water molecules, the total work done is
Wtot = 18. 9 ×10− 25 ×1022 =18 .9×10−3 J
Related Topics