Electric Field

Electric Field

The interaction between two charges is determined by Coulomb’s law. How does the interaction itself occur? Consider a point charge kept at a point in space. If another point charge is placed at some distance from the first point charge, it experiences either an attractive force or repulsive force. This is called ‘action at a distance’. But how does the second charge know about existence of the first charge which is located at some distance away from it? To answer this question, Michael Faraday introduced the concept of field.

According to Faraday, every charge in the universe creates an electric field in the surrounding space, and if another charge is brought into its field, it will interact with the electric field at that point and will experience a force. It may be recalled that the interaction of two masses is similarly explained using the concept of gravitational field (Refer unit 6, volume 2, XI physics). Both the electric and gravitational forces are non-contact forces, hence the field concept is required to explain action at a distance.

Consider a source point charge q located at a point in space. Another point charge q_o (test charge) is placed at some point P which is at a distance r from the charge q. The electrostatic force experienced by the charge q_o due to q is given by Coulomb’s law.

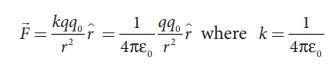
The charge q creates an electric field in the surrounding space. The electric field at the point P at a distance r from the point charge q is the force experienced by a unit charge and is given by

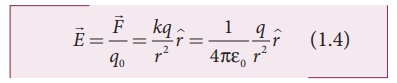
Here ^r is the unit vector pointing from q to the point of interest P. The electric field is a vector quantity and its SI unit is Newton per Coulomb (NC^-1).

Important aspects of Electric field

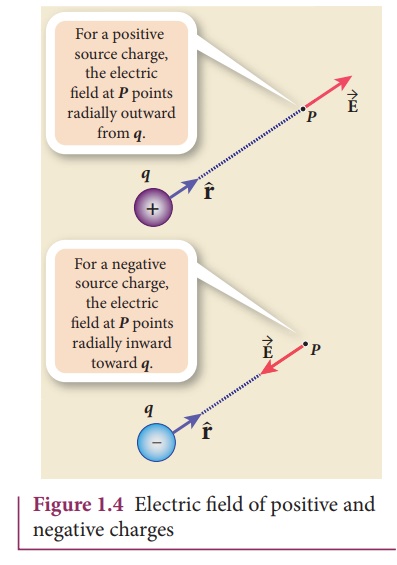
(i) If the charge q is positive then the electric field points away from the source charge and if q is negative, the electric field points towards the source charge q. This is shown in the Figure 1.4.

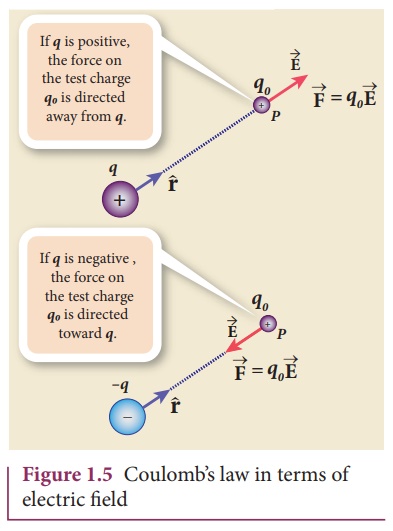
(ii) If the electric field at a point P is , then the force experienced by the test charge q_o placed at the point P is

This is Coulomb’s law in terms of electric field. This is shown in Figure 1.5

(iii) The equation (1.4) implies that the electric field is independent of the test charge q_o and it depends only on the source charge q.

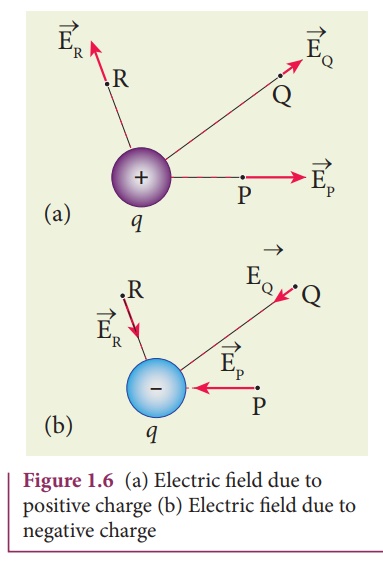
(iv) Since the electric field is a vector quantity, at every point in space, this field has unique direction and magnitude as shown in Figures 1.6(a) and (b). From equation (1.4), we can infer that as distance increases, the electric field decreases in magnitude.

Note that in Figures 1.6 (a) and (b) the length of the electric field vector is shown for three different points. The strength or magnitude of the electric field at point P is stronger than at the points Q and R because the point P is closer to the source charge.

(v) In the definition of electric field, it is assumed that the test charge q₀ is taken sufficiently small, so that bringing this test charge will not move the source charge. In other words, the test charge is made sufficiently small such that it will not modify the electric field of the source charge.

(vi) The expression (1.4) is valid only for point charges. For continuous and finite size charge distributions, integration techniques must be used These will be explained later in the same section. However, this expression can be used as an approximation for a finite-sized charge if the test point is very far away from the finite sized source charge. Note that we similarly treat the Earth as a point mass when we calculate the gravitational field of the Sun on the Earth (refer unit 6, volume 2, XI physics).

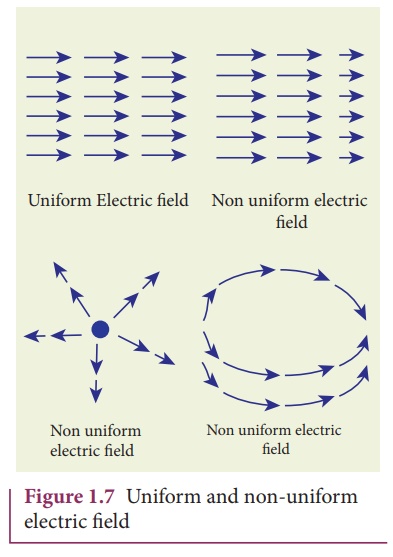
(vii) There are two kinds of the electric field: uniform (constant) electric field and non-uniform electric field. Uniform electric field will have the same direction and constant magnitude at all points in space. Non-uniform electric field will have different directions or different magnitudes or both at different points in space. The electric field created by a point charge is basically a non uniform electric field. This non-uniformity arises, both in direction and magnitude, with the direction being radially outward (or inward) and the magnitude changes as distance increases. These are shown in Figure 1.7.

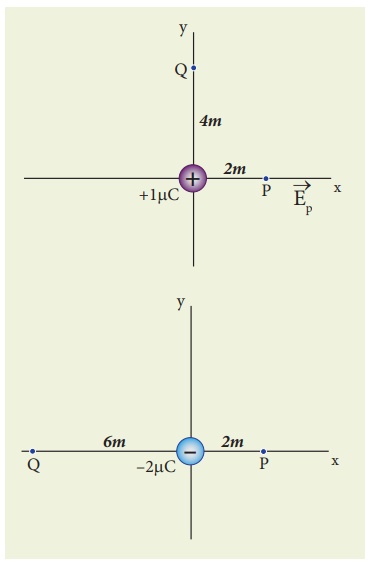
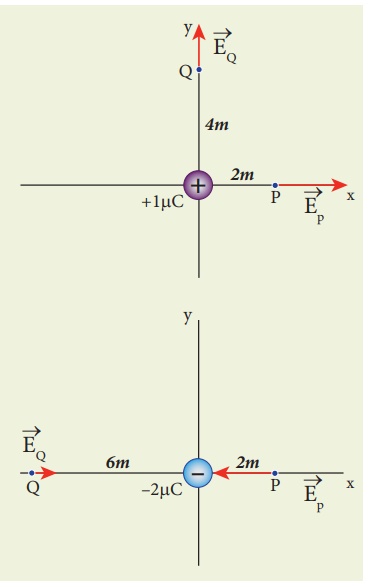
EXAMPLE 1.6

Calculate  the electric field at points P, Q for the following two cases, as shown in the figure.

(a) A positive point charge +1 µC is placed at the origin

(b) A negative point charge -2 µC is placed at the origin

Solution

Case (a)

The magnitude of the electric field at point P is

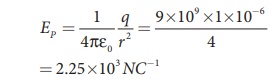
Since the source charge is positive, the electric field points away from the charge. So the electric field at the point P is given by

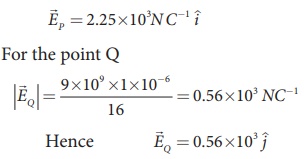
Case (b)

The magnitude of the electric field at point P

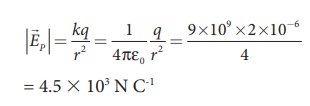
Since the source charge is negative, the electric field points towards the charge. So the electric field at the point P is given by

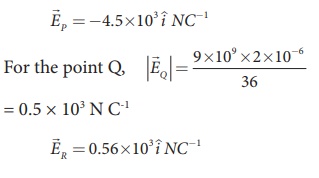
At the point Q the electric field is directed along the positive x-axis.