Chapter: 12th Physics : Electrostatics
Electric Field and Electric Field Lines: Solved Example Problems
EXAMPLE 1.6
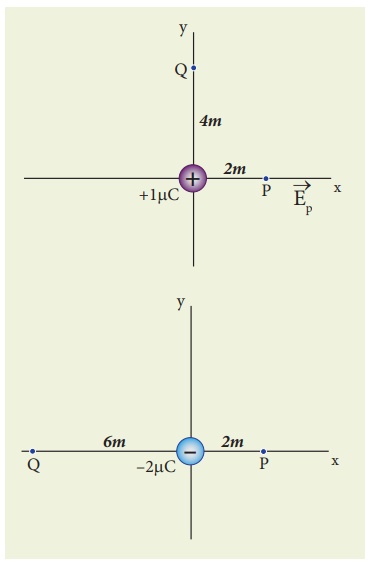
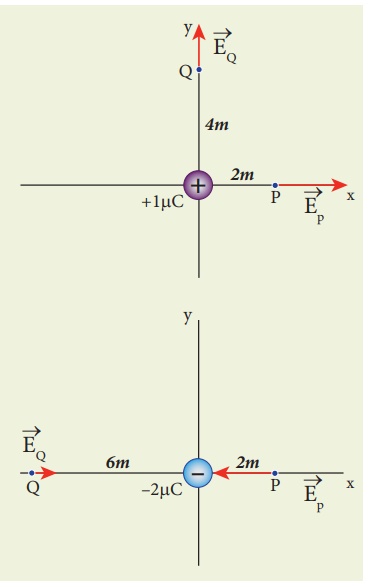
Calculate the electric field at points P, Q for the following two cases, as shown in the figure.
(a) A positive point charge +1 µC is placed at the origin
(b) A negative point charge -2 µC is placed at the origin
Solution
Case (a)
The magnitude of the electric field at point P is
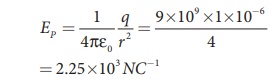
Since the source charge is positive, the electric field points away from the charge. So the electric field at the point P is given by
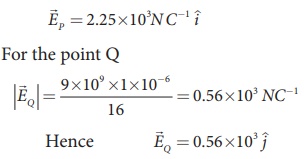
Case (b)
The magnitude of the electric field at point P
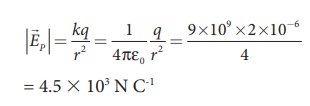
Since the source charge is negative, the electric field points towards the charge. So the electric field at the point P is given by
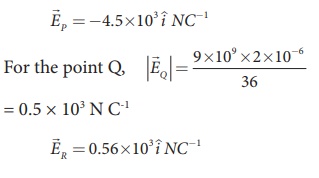
At the point Q the electric field is directed along the positive x-axis.
EXAMPLE 1.7
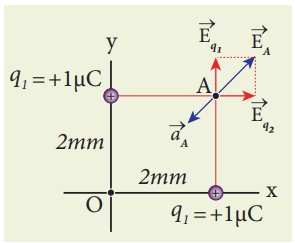
Consider the charge configuration as shown in the figure. Calculate the electric field at point A. If an electron is placed at points A, what is the acceleration experienced by this electron? (mass of the electron = 9.1 × 10-31 kg and charge of electron = −1.6 × 10-19 C)

Solution
By using superposition principle, the net electric field at point A is

where r1A and r2A are the distances of point A from the two charges respectively.
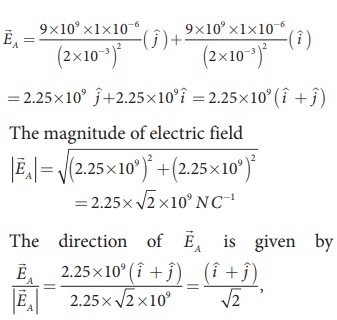
which is the unit vector along OA as shown in the figure.
The acceleration experienced by an electron placed at point A is
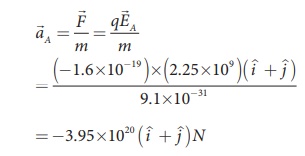
The electron is accelerated in a direction exactly opposite to ![]() A.
A.
EXAMPLE 1.8
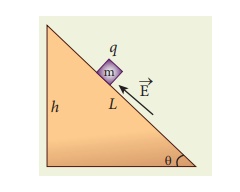
A block of mass m and positive charge q is placed on an insulated frictionless inclined plane as shown in the figure. A uniform electric field E is applied parallel to the inclined surface such that the block is at rest. Calculate the magnitude of the electric field E.
Solution
Note: A similar problem is solved in XIth Physics volume I, unit 3 section 3.3.2.
There are three forces that acts on the mass m:
(i) The downward gravitational force exerted by the Earth (mg)
(ii) The normal force exerted by the inclined surface (N)
(iii) The Coulomb force given by uniform electric field (qE)
The free body diagram for the mass m is drawn below.

A convenient inertial coordinate system is located in the inclined surface as shown in the figure. The mass m has zero net acceleration both in x and y-direction.
Along x-direction, applying Newton’s second law, we have
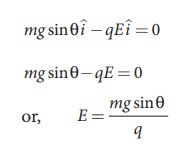
Note that the magnitude of the electric field is directly proportional to the mass m and inversely proportional to the charge q. It implies that, if the mass is increased by keeping the charge constant, then a strong electric field is required to stop the object from sliding. If the charge is increased by keeping the mass constant, then a weak electric field is sufficient to stop the mass from sliding down the plane.
The electric field also can be expressed in terms of height and the length of the inclined surface of the plane.
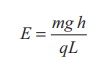
EXAMPLE 1.9
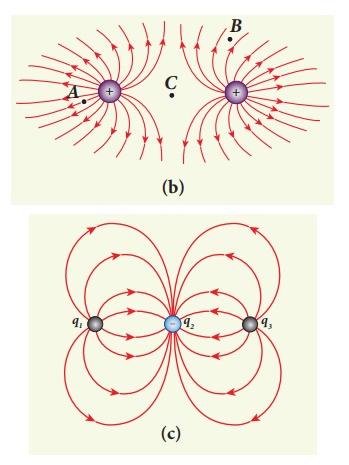
The following pictures depict electric field lines for various charge configurations.
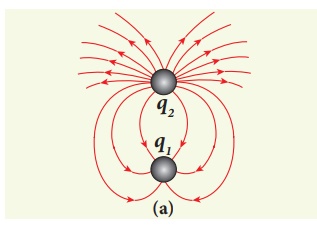
(i) In figure (a) identify the signs of two charges and find the ratio |q1 / q2|
(ii) In figure (b), calculate the ratio of two positive charges and identify the strength of the electric field at three points A, B, and C
(iii) Figure (c) represents the electric field lines for three charges. If q2 = -20 nC, then calculate the values of q1 and q3
Solution
(i) The electric field lines start at q2 and end at q1. In figure (a), q2 is positive and q1 is negative. The number of lines starting from q2 is 18 and number of the lines ending at q1 is 6. So q2 has greater magnitude. The ratio of |q1/ q2| = N1/ N2 = 6/18 = 1/3 . It implies that |q2| = 3|q1|
(ii) In figure (b), the number of field lines emanating from both positive charges are equal (N=18). So the charges are equal. At point A, the electric field lines are denser compared to the lines at point B. So the electric field at point A is greater in magnitude compared to the field at point B. Further, no electric field line passes through C, which implies that the resultant electric field at C due to these two charges is zero.
(iii) In the figure (c), the electric field lines start at q1 and q3 and end at q2. This implies that q1 and q3 are positive charges. The ratio of the number of field lines is | q1 / q2 | = 8/16 = | q3 / q2 | = 1/2 , implying that q1and q3are half of the magnitude of q2. So q1 = q3 = +10 nC.
Related Topics