Physics - Electrostatics: Exercises and Example Solved Problems | 12th Physics : Electrostatics
Chapter: 12th Physics : Electrostatics
Electrostatics: Exercises and Example Solved Problems
Exercises
1. When two objects are rubbed with each other, approximately a charge of 50 nC can be produced in each object. Calculate the number of electrons that must be transferred to produce this charge.
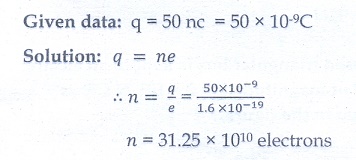
Ans: 31.25 × 1010 electrons
2. The total number of electrons in the human body is typically in the order of 1028. Suppose, due to some reason, you and your friend lost 1% of this number of electrons. Calculate the electrostatic force between you and your friend separated at a distance of 1m. Compare this with your weight. Assume mass of each person is 60 kg and use point charge approximation.

Ans: Fe = 9 × 1061 N, W = 588 N
3. Five identical charges Q are placed equidistant on a semicircle as shown in the figure. Another point charge q is kept at the center of the circle of radius R. Calculate the electrostatic force experienced by the charge q.
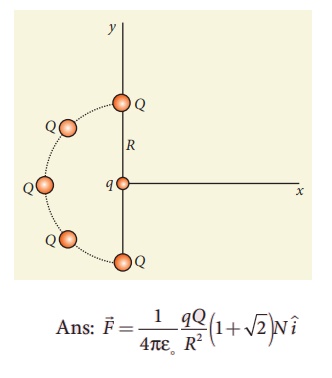

4. Suppose a charge +q on Earth’s surface and another +q charge is placed on the surface of the Moon. (a) Calculate the value of q required to balance the gravitational attraction between Earth and Moon (b) Suppose the distance between the Moon and Earth is halved, would the charge q change?
(Take mE = 5.9 × 1024 kg, mM = 7.9 × 1022 kg)

Ans: (a) q ≈ +5.64 × 1013 C, (b) no change
5. Draw the free body diagram for the following charges as shown in the figure (a), (b) and (c).
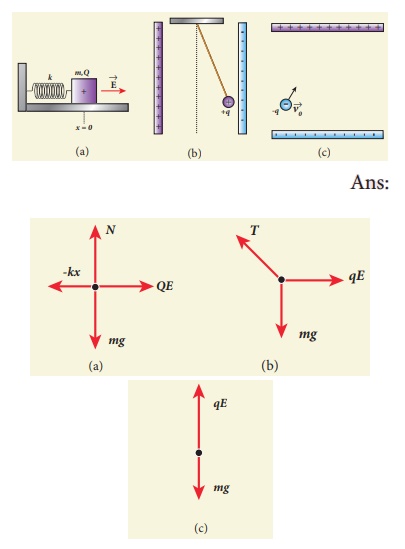
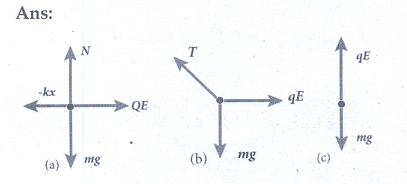
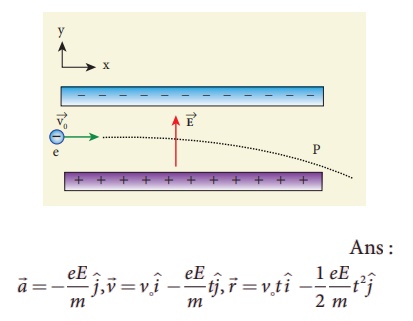
6. Consider an electron travelling with a speed vo and entering into a uniform electric field ![]() which is perpendicular to
which is perpendicular to ![]() as shown in the Figure. Ignoring gravity, obtain the electron’s acceleration, velocity and position as functions of time.
as shown in the Figure. Ignoring gravity, obtain the electron’s acceleration, velocity and position as functions of time.

7. A closed triangular box is kept in an electric field of magnitude E = 2 × 103 N C-1 as shown in the figure.
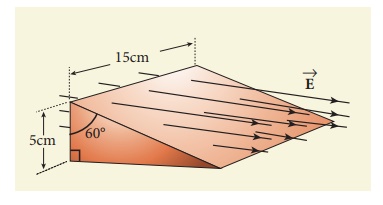
Calculate the electric flux through the (a) vertical rectangular surface (b) slanted surface and (c) entire surface.

Ans: (a) 15 Nm2 C-1 (b) 15 Nm2 C-1 (c) zero
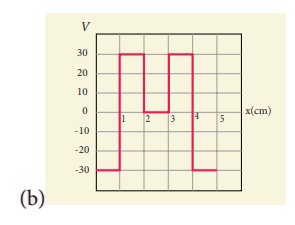
8. The electrostatic potential is given as a function of x in figure (a) and (b). Calculate the corresponding electric fields in regions A, B, C and D. Plot the electric field as a function of x for the figure (b).
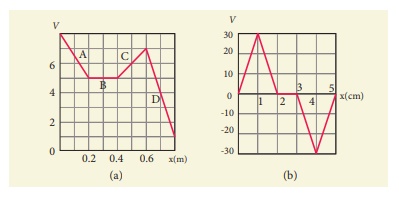

Ans: (a) EX = 15 Vm-1 (region A), EX = -10 Vm-1 (region C)
EX = 0 (region B), EX = 30 Vm-1 (region D)
9. A spark plug in a bike or a car is used to ignite the air-fuel mixture in the engine. It consists of two electrodes separated by a gap of around 0.6 mm gap as shown in the figure.

To create the spark, an electric field of magnitude 3 × 106 Vm-1 is required. (a) What potential difference must be applied to produce the spark? (b) If the gap is increased, does the potential difference increase, decrease or remains the same? (c) find the potential difference if the gap is 1 mm.

Ans: (a) 1800 V, (b) increases (c) 3000 V
10. A point charge of +10 µC is placed at a distance of 20 cm from another identical point charge of +10 µC. A point charge of -2 µC is moved from point a to b as shown in the figure. Calculate the change in potential energy of the system? Interpret your result.
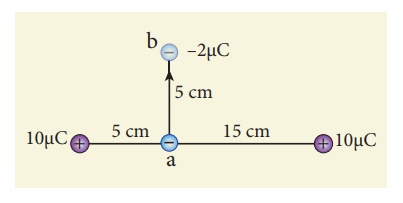

Ans: ∆U = -3.246 J, negative sign implies that to move the charge -2µC no external work is required. System spends its stored energy to move the charge from point a to point b.
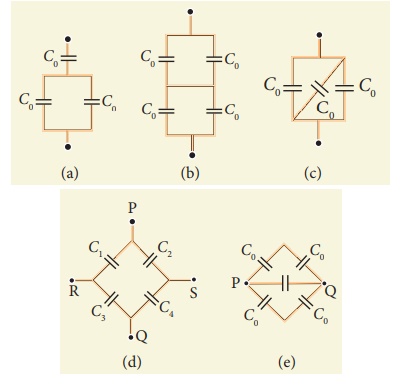
11. Calculate the resultant capacitances for each of the following combinations of capacitors.


12. An electron and a proton are allowed to fall through the separation between the plates of a parallel plate capacitor of voltage 5 V and separation distance h = 1 mm as shown in the figure.
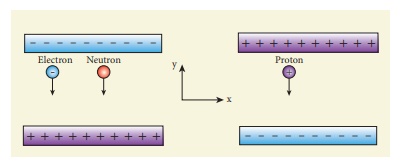
(a) Calculate the time of flight for both electron and proton
(b) Suppose if a neutron is allowed to fall, what is the time of flight?
(c) Among the three, which one will reach the bottom first?
(Take mp = 1.6 x 10-27 kg, me = 9.1 x 10-31 kg and g = 10 m s-2)
Ans:

(c) electron will reach first
13. During a thunder storm, the movement of water molecules within the clouds creates friction, partially causing the bottom part of the clouds to become negatively charged. This implies that the bottom of the cloud and the ground act as a parallel plate capacitor. If the electric field between the cloud and ground exceeds the dielectric breakdown of the air (3 × 106 Vm-1 ), lightning will occur.

(a) If the bottom part of the cloud is 1000 m above the ground, determine the electric potential difference that exists between the cloud and ground.
(b) In a typical lightning phenomenon, around 25C of electrons are transferred from cloud to ground. How much electrostatic potential energy is transferred to the ground?
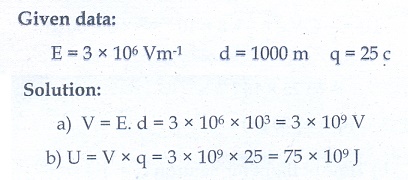
Ans: (a) V = 3 × 109 V, (b) U = 75 × 109 J
14. For the given capacitor configuration
(a) Find the charges on each capacitor
(b) potential difference across them
(c) energy stored in each capacitor
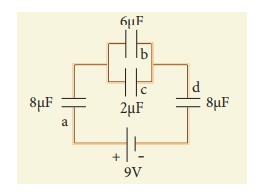
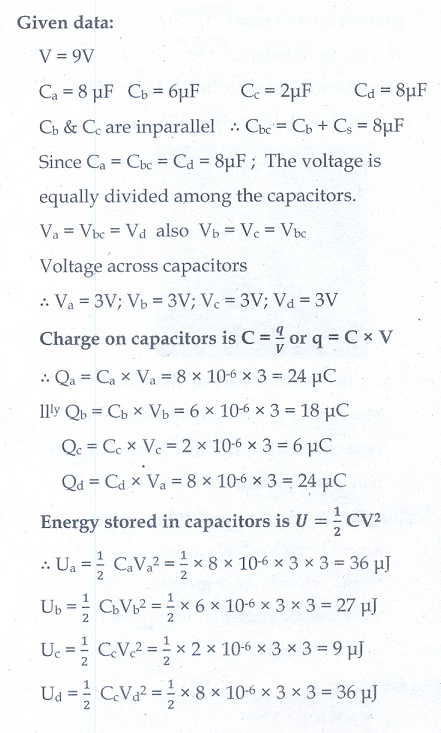
Ans:
Qa = 24 µC, Qb = 18 µC,
Qc = 6 µC, Qd = 24 µC
Va = 3V, Vb = 3V,
Vc = 3V, Vd = 3V,
Ua = 36 µJ, Ub = 27 µJ,
Uc = 9 µJ, Ud = 36 µJ
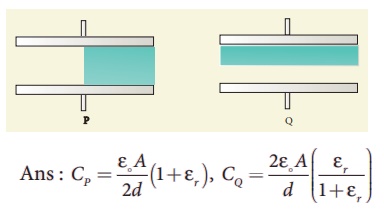
15. Capacitors P and Q have identical cross sectional areas A and separation d. The space between the capacitors is filled with a dielectric of dielectric constant εr as shown in the figure. Calculate the capacitance of capacitors P and Q.

EXAMPLE 1.1
Calculate the number of electrons in one coulomb of negative charge.
Solution
According to the quantisation of charge
q = ne
Here q = 1C. So the number of electrons in 1 coulomb of charge is
n = q/e = IC/1.6x10-10 = 6.25x1018 electrons
EXAMPLE 1.2
Consider two point charges q1 and q2 at rest as shown in the figure.
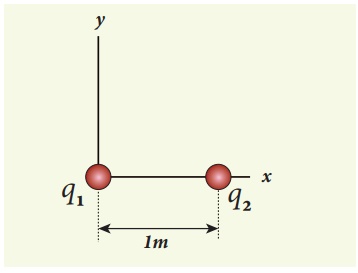
They are separated by a distance of 1m. Calculate the force experienced by the two charges for the following cases:
(a) q1 = +2μC and q2 = +3μC
(b) q1 = +2μC and q2 = -3μC
(c) q1= +2μC and q2 = -3μC kept in water (εr = 80)
Solution
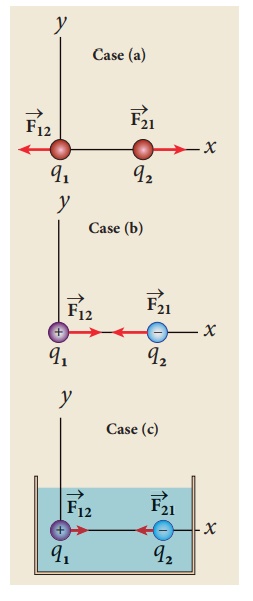



EXAMPLE 1.3
Two small-sized identical equally charged spheres, each having mass 1 mg are hanging in equilibrium as shown in the figure. The length of each string is 10 cm and the angle θ is 7° with the vertical. Calculate the magnitude of the charge in each sphere.
(Take g = 10 ms−2)
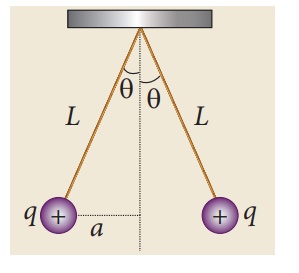
Solution
If the two spheres are neutral, the angle between them will be 0o when hanged vertically. Since they are positively charged spheres, there will be a repulsive force between them and they will be at equilibrium with each other at an angle of 7° with the vertical. At equilibrium, each charge experiences zero net force in each direction. We can draw a free body diagram for one of the charged spheres and apply Newton’s second law for both vertical and horizontal directions.
The free body diagram is shown below.
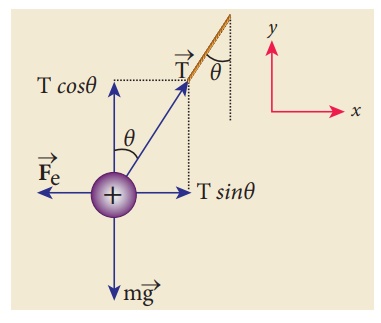
In the x-direction, the acceleration of the charged sphere is zero.
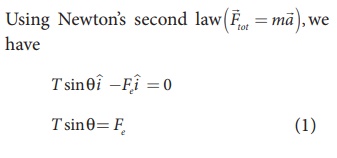
Here T is the tension acting on the charge due to the string and Fe is the electrostatic force between the two charges.
In the y-direction also, the net acceleration experienced by the charge is zero.

EXAMPLE 1.4
Calculate the electrostatic force and gravitational force between the proton and the electron in a hydrogen atom. They are separated by a distance of 5.3 × 10-11 m. The magnitude of charges on the electron and proton are 1.6 × 10-19 C. Mass of the electron is me = 9.1 × 10-31 kg and mass of proton is mp = 1.6 × 10-27 kg.
Solution
The proton and the electron attract each other. The magnitude of the electrostatic force between these two particles is given by
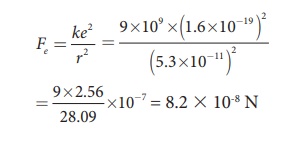
The gravitational force between the proton and the electron is attractive. The magnitude of the gravitational force between these particles is

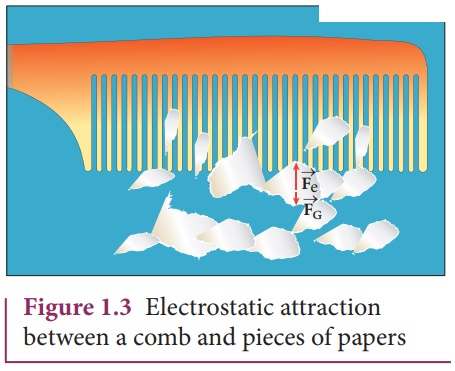
The electrostatic force between a proton and an electron is enormously greater than the gravitational force between them. Thus the gravitational force is negligible when compared with the electrostatic force in many situations such as for small size objects and in the atomic domain. This is the reason why a charged comb attracts an uncharged piece of paper with greater force even though the piece of paper is attracted downward by the Earth. This is shown in Figure 1.3
EXAMPLE 1.5
Consider four equal charges q1,q2, q3 and q4 = q = +1μC located at four different points on a circle of radius 1m, as shown in the figure. Calculate the total force acting on the charge q1 due to all the other charges.

Solution
According to the superposition principle, the total electrostatic force on charge q1 is the vector sum of the forces due to the other charges,
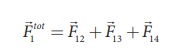
The following diagram shows the direction of each force on the charge q1.
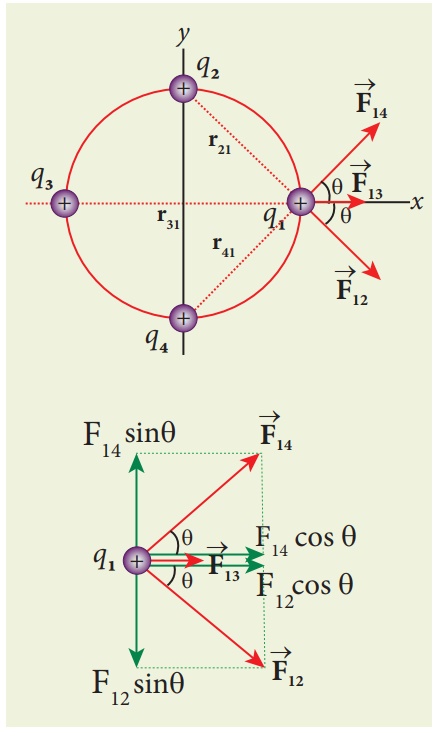
The charges q2 and q4 are equi-distant from q1. As a result the strengths (magnitude) of the forces ![]() and
and ![]() are the same even though their directions are different. Therefore the vectors representing these two forces are drawn with equal lengths. But the charge q3 is located farther compared to q2 and q4. Since the strength of the electrostatic force decreases as distance increases, the strength of the force
are the same even though their directions are different. Therefore the vectors representing these two forces are drawn with equal lengths. But the charge q3 is located farther compared to q2 and q4. Since the strength of the electrostatic force decreases as distance increases, the strength of the force ![]() is lesser than that of forces
is lesser than that of forces ![]() and
and ![]() . Hence the vector representing the force
. Hence the vector representing the force ![]() is drawn with smaller length compared to that for forces
is drawn with smaller length compared to that for forces ![]() and
and ![]() .
.
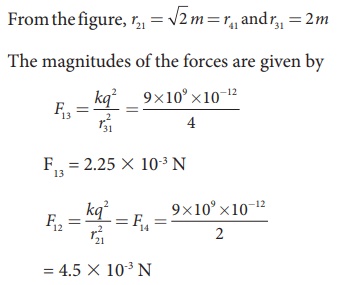
From the figure, the angle θ = 45º. In terms of the components, we have
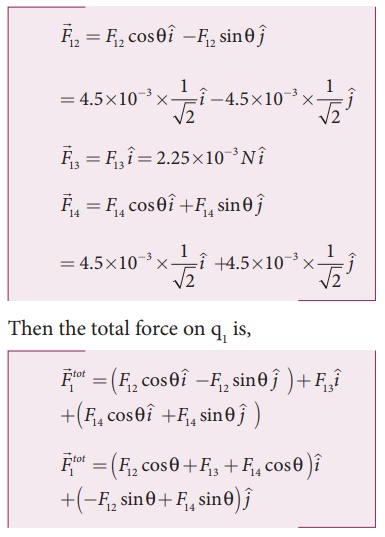
Since F12 = F14, the jth component is zero.
Hence we have
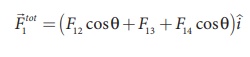
substituting the values in the above equation,
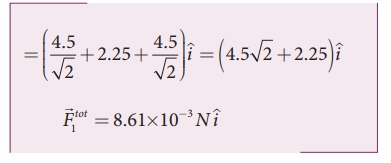
The resultant force is along the positive x axis.
Electric Field and Electric Field Lines: Solved Example Problems
EXAMPLE 1.6
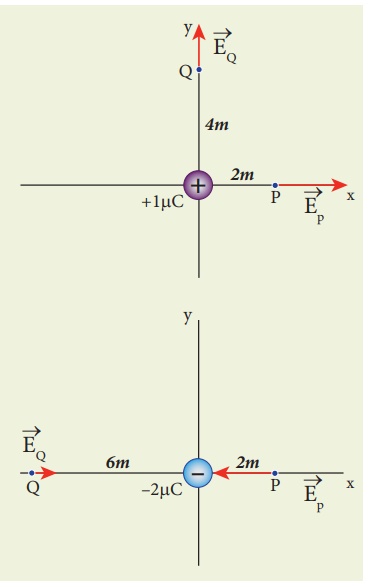
Calculate the electric field at points P, Q for the following two cases, as shown in the figure.
(a) A positive point charge +1 µC is placed at the origin
(b) A negative point charge -2 µC is placed at the origin
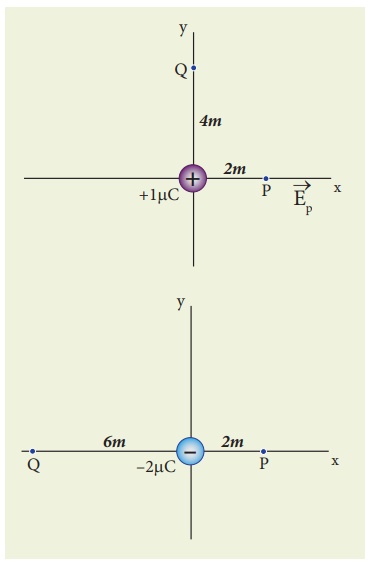
Solution
Case (a)
The magnitude of the electric field at point P is
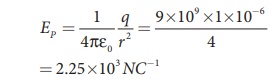
Since the source charge is positive, the electric field points away from the charge. So the electric field at the point P is given by
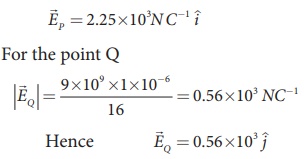
Case (b)
The magnitude of the electric field at point P
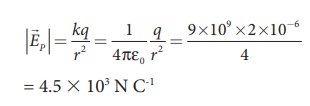
Since the source charge is negative, the electric field points towards the charge. So the electric field at the point P is given by
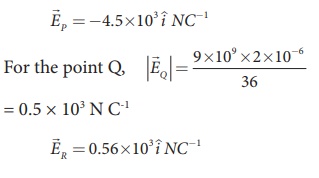
At the point Q the electric field is directed along the positive x-axis.
EXAMPLE 1.7
Consider the charge configuration as shown in the figure. Calculate the electric field at point A. If an electron is placed at points A, what is the acceleration experienced by this electron? (mass of the electron = 9.1 × 10-31 kg and charge of electron = −1.6 × 10-19 C)

Solution
By using superposition principle, the net electric field at point A is

where r1A and r2A are the distances of point A from the two charges respectively.
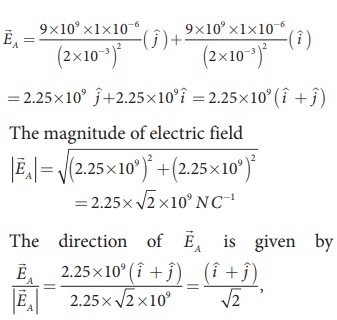
which is the unit vector along OA as shown in the figure.
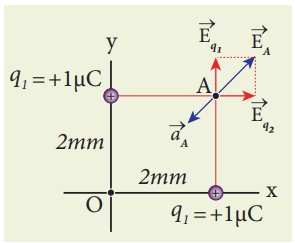
The acceleration experienced by an electron placed at point A is
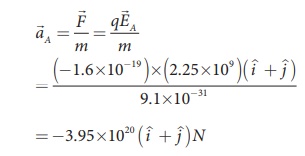
The electron is accelerated in a direction exactly opposite to ![]() A.
A.
EXAMPLE 1.8
A block of mass m and positive charge q is placed on an insulated frictionless inclined plane as shown in the figure. A uniform electric field E is applied parallel to the inclined surface such that the block is at rest. Calculate the magnitude of the electric field E.
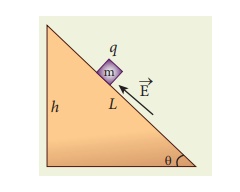
Solution
Note: A similar problem is solved in XIth Physics volume I, unit 3 section 3.3.2.
There are three forces that acts on the mass m:
(i) The downward gravitational force exerted by the Earth (mg)
(ii) The normal force exerted by the inclined surface (N)
(iii) The Coulomb force given by uniform electric field (qE)
The free body diagram for the mass m is drawn below.

A convenient inertial coordinate system is located in the inclined surface as shown in the figure. The mass m has zero net acceleration both in x and y-direction.
Along x-direction, applying Newton’s second law, we have
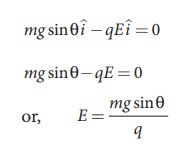
Note that the magnitude of the electric field is directly proportional to the mass m and inversely proportional to the charge q. It implies that, if the mass is increased by keeping the charge constant, then a strong electric field is required to stop the object from sliding. If the charge is increased by keeping the mass constant, then a weak electric field is sufficient to stop the mass from sliding down the plane.
The electric field also can be expressed in terms of height and the length of the inclined surface of the plane.
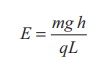
EXAMPLE 1.9
The following pictures depict electric field lines for various charge configurations.
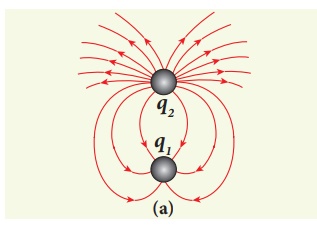
(i) In figure (a) identify the signs of two charges and find the ratio |q1 / q2|
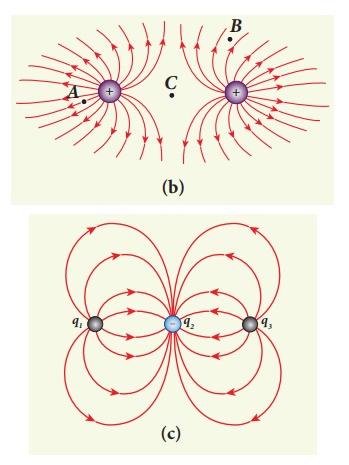
(ii) In figure (b), calculate the ratio of two positive charges and identify the strength of the electric field at three points A, B, and C
(iii) Figure (c) represents the electric field lines for three charges. If q2 = -20 nC, then calculate the values of q1 and q3
Solution
(i) The electric field lines start at q2 and end at q1. In figure (a), q2 is positive and q1 is negative. The number of lines starting from q2 is 18 and number of the lines ending at q1 is 6. So q2 has greater magnitude. The ratio of |q1/ q2| = N1/ N2 = 6/18 = 1/3 . It implies that |q2| = 3|q1|
(ii) In figure (b), the number of field lines emanating from both positive charges are equal (N=18). So the charges are equal. At point A, the electric field lines are denser compared to the lines at point B. So the electric field at point A is greater in magnitude compared to the field at point B. Further, no electric field line passes through C, which implies that the resultant electric field at C due to these two charges is zero.
(iii) In the figure (c), the electric field lines start at q1 and q3 and end at q2. This implies that q1 and q3 are positive charges. The ratio of the number of field lines is | q1 / q2 | = 8/16 = | q3 / q2 | = 1/2 , implying that q1and q3are half of the magnitude of q2. So q1 = q3 = +10 nC.
Electric Dipole : Solved Example Problems
EXAMPLE 1.10
Calculate the electric dipole moment for the following charge configurations.
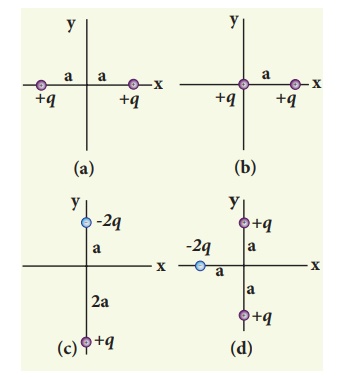
Solution
Case (a) The position vector for the +q on the positive x-axis is ai and position vector for the +q charge the negative x axis is -a i ^ . So the dipole moment is,
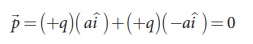
Case (b) In this case one charge is placed at the origin, so its position vector is zero. Hence only the second charge +q with position vector ai contributes to the dipole moment, which is ![]() = qa
= qa![]() .
.
From both cases (a) and (b), we can infer that in general the electric dipole moment depends on the choice of the origin and charge configuration. But for one special case, the electric dipole moment is independent of the origin. If the total charge is zero, then the electric dipole moment will be the same irrespective of the choice of the origin. It is because of this reason that the electric dipole moment of an electric dipole (total charge is zero) is always directed from –q to +q, independent of the choice of the origin.
Case (c) 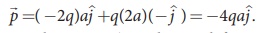 . Note that in this case p is directed from -2q to +q.
. Note that in this case p is directed from -2q to +q.
Case (d) 
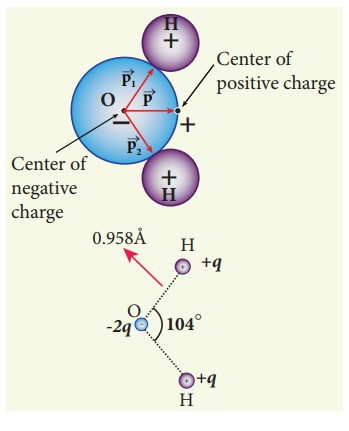
The water molecule (H2O) has this charge configuration. The water molecule has three atoms (two H atom and one O atom). The centers of positive (H) and negative (O) charges of a water molecule lie at different points, hence it possess permanent dipole moment. The O-H bond length is 0.958 × 10-10 m due to which the electric dipole moment of water molecule has the magnitude p = 6.1 x 10-30 Cm. The electric dipole moment ![]() is directed from center of negative charge to the center of positive charge, as shown in the figure.
is directed from center of negative charge to the center of positive charge, as shown in the figure.
EXAMPLE 1.11
A sample of HCl gas is placed in a uniform electric field of magnitude 3 × 104 N C-1. The dipole moment of each HCl molecule is 3.4 × 10-30 Cm. Calculate the maximum torque experienced by each HCl molecule.
Solution
The maximum torque experienced by the dipole is when it is aligned perpendicular to the applied field.
τmax = pE sin 90 = 3 .4×10−30 ×3 ×104 N m
τmax = 10.2 ×10−26 N m
Electric potential due to a point charge
EXAMPLE 1.12
(a) Calculate the electric potential at points P and Q as shown in the figure below.
(b) Suppose the charge +9µC is replaced by -9µC find the electrostatic potentials at points P and Q
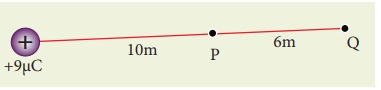
( c ) Calculate the work done to bring a test charge +2µC from infinity to the point P. Assume the charge +9µC is held fixed at origin and +2µC is brought from infinity to P.
Solution
(a) Electric potential at point P is given by
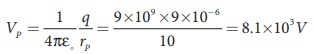
Electric potential at point Q is given by
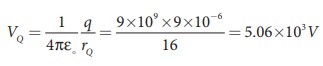
Note that the electric potential at point Q is less than the electric potential at point P. If we put a positive charge at P, it moves from P to Q. However if we place a negative charge at P it will move towards the charge +9µC.
The potential difference between the points P and Q is given by
∆V = VP −VQ = +3 .04 ×103V
(b) Suppose we replace the charge +9 µC by -9 µC, then the corresponding potentials at the points P and Q are,
VP = −8 . 1×103 V , VQ =− 5.06 ×103V
Note that in this case electric potential at the point Q is higher than at point P.
The potential difference or voltage between the points P and Q is given by
∆V = VP −VQ = −3 .04 ×103V
(c) The electric potential V at a point P due to some charge is defined as the work done by an external force to bring a unit positive charge from infinity to P. So to bring the q amount of charge from infinity to the point P, work done is given as follows.
W = qV
WQ = 2 ×10− 6 × 5. 06 ×103 J = 10 .12 ×10−3 J.
EXAMPLE 1.13
Consider a point charge +q placed at the origin and another point charge -2q placed at a distance of 9 m from the charge +q. Determine the point between the two charges at which electric potential is zero.
Solution
According to the superposition principle, the total electric potential at a point is equal to the sum of the potentials due to each charge at that point.
Consider the point at which the total potential zero is located at a distance x from the charge +q as shown in the figure.

Relation between electric field and potential
EXAMPLE 1.14
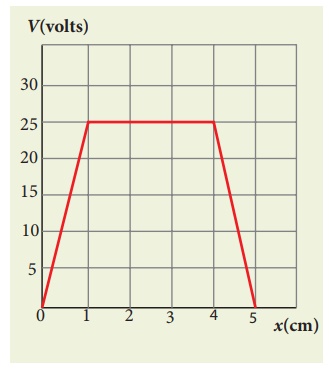
The following figure represents the electric potential as a function of x – coordinate. Plot the corresponding electric field as a function of x.
Solution
In the given problem, since the potential depends only on x, we can use 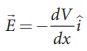 (the other two terms ∂V/∂y and ∂V/∂z are zero)
(the other two terms ∂V/∂y and ∂V/∂z are zero)
From 0 to 1 cm, the slope is constant and so dV/dx = 25V cm−1.
So ![]() = −25V cm−1
= −25V cm−1 ![]()
From 1 to 4 cm, the potential is constant, V = 25 V. It implies that dV/dx = 0. So ![]() = 0
= 0
From 4 to 5 cm, the slope dV/dx = −25V cm−1.
So ![]() = +25V cm−1
= +25V cm−1 ![]()
The plot of electric field for the various points along the x axis is given below.

Electrostatic potential energy for collection of point charges
EXAMPLE 1.15
Four charges are arranged at the corners of the square PQRS of side a as shown in the figure.(a) Find the work required to assemble these charges in the given configuration. (b) Suppose a charge q′ is brought to the center of the square, by keeping the four charges fixed at the corners, how much extra work is required for this?
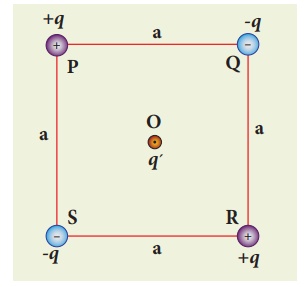
Solution
(a) The work done to arrange the charges in the corners of the square is independent of the way they are arranged. We can follow any order.
(i) First, the charge +q is brought to the corner P. This requires no work since no charge is already present, WP = 0
(ii) Work required to bring the charge –q to the corner Q = (-q) x potential at a point Q due to +q located at a point P.
WQ = −q × 1/4πε . q/ = − 1/4πε . q2/a

(iii) Work required to bring the charge +q to the corner R= q × potential at the point R due to charges at the point P and Q.

(iv) Work required to bring the fourth charge –q at the position S = q × potential at the point S due the all the three charges at the point P, Q and R
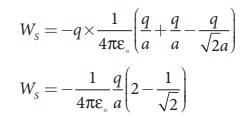
(b) Work required to bring the charge q′ to the center of the square = q′ × potential at the center point O due to all the four charges in the four corners
The potential created by the two +q charges are canceled by the potential created by the -q charges which are located in the opposite corners. Therefore the net electric potential at the center O due to all the charges in the corners is zero.
Hence no work is required to bring any charge to the point O. Physically this implies that if any charge q′ when brought close to O, then it moves to the point O without any external force.
Electrostatic potential energy of a dipole in a uniform electric field
EXAMPLE 1.16
A water molecule has an electric dipole moment of 6.3 × 10-30 Cm. A sample contains 1022 water molecules, with all the dipole moments aligned parallel to the external electric field of magnitude 3 × 105 N C-1. How much work is required to rotate all the water molecules from θ = 0º to 90º?
Solution
When the water molecules are aligned in the direction of the electric field, it has minimum potential energy. The work done to rotate the dipole from θ = 0º to 90º is equal to the potential energy difference between these two configurations.
W= ∆U =U (90º)−U (0º)
From the equation (1.51), we write U = − pE cosθ, Next we calculate the work done to rotate one water molecule from θ = 0º to 90º.
For one water molecule
W = −pE cos 90º + pE cos0º = pE
W = 6 . 3×10− 30 × 3 ×105 = 18 .9×10−25 J
For 1022 water molecules, the total work done is
Wtot = 18. 9 ×10− 25 ×1022 =18 .9×10−3 J
Electric Flux: Solved Example Problems
EXAMPLE 1.17
Calculate the electric flux through the rectangle of sides 5 cm and 10 cm kept in the region of a uniform electric field 100 NC-1. The angle θ is 60o. Suppose θ becomes zero, what is the electric flux?
Solution
The electric flux
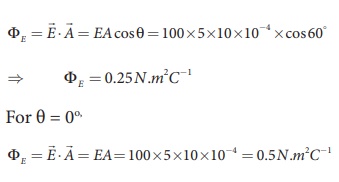
Gauss law: Solved Example Problems
EXAMPLE 1.18
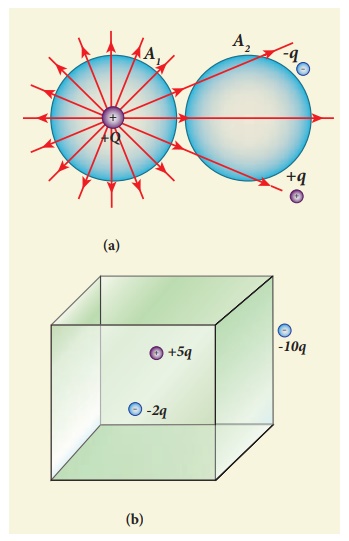
(i) In figure (a), calculate the electric flux through the closed areas A1 and A2.
(ii) In figure (b), calculate the electric flux through the cube
Solution
(i) In figure (a), the area A1 encloses the charge Q. So electric flux through this closed surface A1 is Q/ ε . But the closed surface A2 contains no charges inside, so electric flux through A2 is zero.
(ii) In figure (b), the net charge inside the cube is 3q and the total electric flux in the cube is therefore ΦE = 3q/ ε .
Note that the charge -10 q lies outside the cube and it will not contribute the total flux through the surface of the cube.
Electrostatic induction: Solved Example Problems
EXAMPLE 1.19
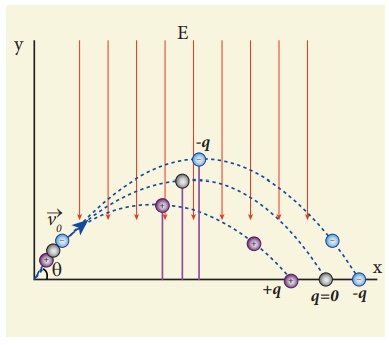
A small ball of conducting material having a charge +q and mass m is thrown upward at an angle θ to horizontal surface with an initial speed vo as shown in the figure. There exists an uniform electric field E downward along with the gravitational field g. Calculate the range, maximum height and time of flight in the motion of this charged ball. Neglect the effect of air and treat the ball as a point mass.
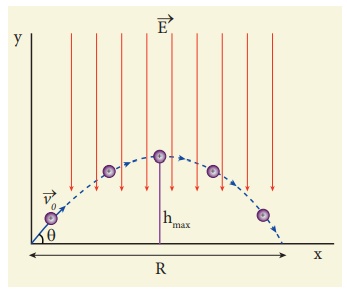
Solution
If the conductor has no net charge, then its motion is the same as usual projectile motion of a mass m which we studied in Kinematics (unit 2, vol-1 XI physics). Here, in this problem, in addition to downward gravitational force, the charge also will experience a downward uniform electrostatic force.
The acceleration of the charged ball due to gravity = -g j ^
The acceleration of the charged ball due to uniform electric field = -qE/m j ^
The total acceleration of charged ball in downward direction
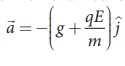
It is important here to note that the acceleration depends on the mass of the object. Galileo’s conclusion that all objects fall at the same rate towards the Earth is true only in a uniform gravitational field. When a uniform electric field is included, the acceleration of a charged object depends on both mass and charge.
But still the acceleration a = ( g + qE/ m ) is constant throughout the motion. Hence we use kinematic equations to calculate the range, maximum height and time of flight.
In fact we can simply replace g by g + qE/m in the usual expressions of range, maximum height and time of flight of a projectile.
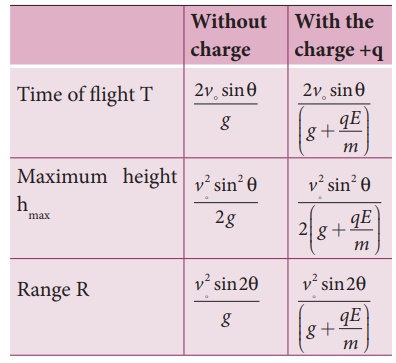
Note that the time of flight, maximum height, range are all inversely proportional to the acceleration of the object. Since ( g + qE/m ) > g for charge +q, the quantities T, hmax, and R will decrease when compared to the motion of an object of mass m and zero net charge. Suppose the charge is –q, then ( g - qE/m ) < g , and the quantities T, hmax and R will increase. Interestingly the trajectory is still parabolic as shown in the figure.
Capacitors: Solved Example Problems
Example 1.20
A parallel plate capacitor has square plates of side 5 cm and separated by a distance of 1 mm. (a) Calculate the capacitance of this capacitor. (b) If a 10 V battery is connected to the capacitor, what is the charge stored in any one of the plates? (The value of εo = 8.85 x 10-12 Nm2 C-2)
Solution
(a) The capacitance of the capacitor is
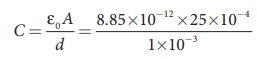
= 221.2 ×10−13 F
C = 22 . 12 ×10−12 F = 22 .12 pF
(b) The charge stored in any one of the plates is Q = CV, Then
= 22 . 12 ×10−12 ×10 = 221.2 ×10−12 C = 221.2 pC
Capacitance of a parallel plate capacitor: Solved Example Problems
Example 1.20
A parallel plate capacitor has square plates of side 5 cm and separated by a distance of 1 mm. (a) Calculate the capacitance of this capacitor. (b) If a 10 V battery is connected to the capacitor, what is the charge stored in any one of the plates? (The value of εo = 8.85 x 10-12 Nm2 C-2)
Solution
(a) The capacitance of the capacitor is
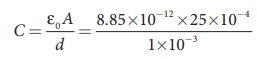
= 221.2 ×10−13 F
C = 22 . 12 ×10−12 F = 22 .12 pF
(b) The charge stored in any one of the plates is Q = CV, Then
= 22 . 12 ×10−12 ×10 = 221.2 ×10−12 C = 221.2 pC
Effect of dielectrics in capacitors: Solved Example Problems
EXAMPLE 1.21
A parallel plate capacitor filled with mica having εr = 5 is connected to a 10 V battery. The area of the parallel plate is 6 m2 and separation distance is 6 mm.
(a) Find the capacitance and stored charge.
(b) After the capacitor is fully charged, the battery is disconnected and the dielectric is removed carefully.
Calculate the new values of capacitance, stored energy and charge.
Solution
(a) The capacitance of the capacitor in the presence of dielectric is

(b) After the removal of the dielectric, since the battery is already disconnected the total charge will not change. But the potential difference between the plates increases. As a result, the capacitance is decreased.
New capacitance is
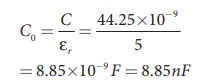
The stored charge remains same and 442.5 nC. Hence newly stored energy is
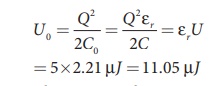
The increased energy is
∆U = 11.05µ J −2.21 µ J = 8.84 µ J
When the dielectric is removed, it experiences an inward pulling force due to the plates. To remove the dielectric, an external agency has to do work on the dielectric which is stored as additional energy. This is the source for the extra energy 8.84 µJ.
Capacitor in series and parallel: Solved Example Problems
EXAMPLE 1.22
Find the equivalent capacitance between P and Q for the configuration shown below in the figure (a).
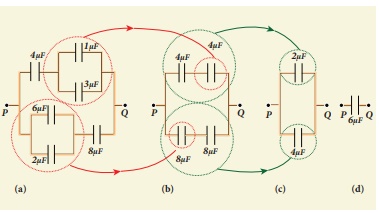
Solution
The capacitors 1 µF and 3µF are connected in parallel and 6µF and 2 µF are also separately connected in parallel. So these parallel combinations reduced to equivalent single capacitances in their respective positions, as shown in the figure (b).
Ceq = 1µF + 3µF = 4µF
Ceq = 6µF + 2µF = 8µF
From the figure (b), we infer that the two 4 µF capacitors are connected in series and the two 8 µF capacitors are connected in series. By using formula for the series, we can reduce to their equivalent capacitances as shown in figure (c).

From the figure (c), we infer that 2µF and 4µF are connected in parallel. So the equivalent capacitance is given in the figure (d).
Ceq = 2µF + 4µF = 6µF
Thus the combination of capacitances in figure (a) can be replaced by a single capacitance 6 µF.
Distribution of charges in a conductor: Solved Example Problems
EXAMPLE 1.23
Two conducting spheres of radius r1 = 8 cm and r2 = 2 cm are separated by a distance much larger than 8 cm and are connected by a thin conducting wire as shown in the figure. A total charge of Q = +100 nC is placed on one of the spheres. After a fraction of a second, the charge Q is redistributed and both the spheres attain electrostatic equilibrium.
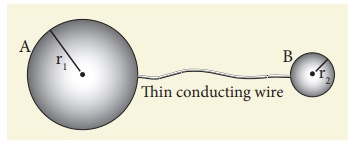
(a) Calculate the charge and surface charge density on each sphere.
(b) Calculate the potential at the surface of each sphere.
Solution
(a) The electrostatic potential on the surface of the sphere A is 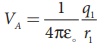
The electrostatic potential on the surface of the sphere A is 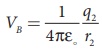
Since VA = VB. We have
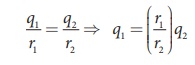
But from the conservation of total charge, Q = q1 + q2, we get q1 = Q – q2. By substituting this in the above equation,
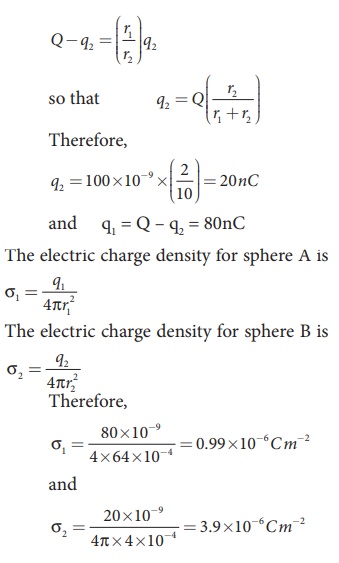
Note that the surface charge density is greater on the smaller sphere compared to the larger sphere (σ2 ≈ 4σ1) which confirms the result σ1 / σ1= r2 / r2.
The potential on both spheres is the same. So we can calculate the potential on any one of the spheres.
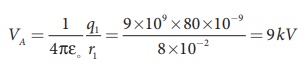
Van de Graaff Generator: Solved Example Problems
EXAMPLE 1.24
Dielectric strength of air is 3 × 106 V m-1. Suppose the radius of a hollow sphere in the Van de Graff generator is R = 0.5 m, calculate the maximum potential difference created by this Van de Graaff generator.
The electric field on the surface of the sphere (by Gauss law) is given by
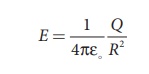
The potential on the surface of the hollow metallic sphere is given by
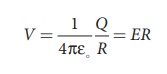
with Vmax = EmaxR
Here Emax = 3 ×106 V/m . So the maximum potential difference created is given by
Vmax = 3 × 106 × 0.5
= 1.5 × 106 V (or) 1.5 million volt
Related Topics