Formula with Solved Example Problems - Gauss law | 12th Physics : Electrostatics
Chapter: 12th Physics : Electrostatics
Gauss law
Gauss law
A positive point charge Q is surrounded by an imaginary sphere of radius r as shown in Figure 1.36. We can calculate the total electric flux through the closed surface of the sphere using the equation (1.58).
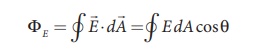
The electric field of the point charge is directed radially outward at all points on the surface of the sphere. Therefore, the direction of the area element d![]() is along the electric field
is along the electric field ![]() and θ = 0° .
and θ = 0° .

The equation (1.61) is called as Gauss’s law. The remarkable point about this result is that the equation (1.61) is equally true for any arbitrary shaped surface which encloses the charge Q and as shown in the Figure 1.37. It is seen that the total electric flux is the same for closed surfaces A1, A2 and A3 as shown in the Figure 1.37.

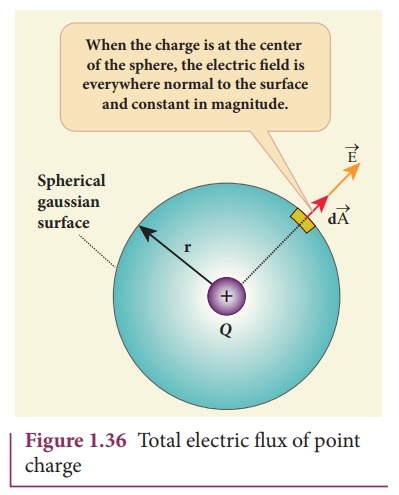
Gauss’s law states that if a charge Q is enclosed by an arbitrary closed surface, then the total electric flux ΦE through the closed surface is
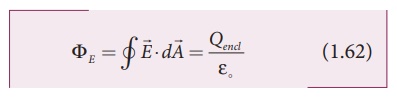
Here Qencl denotes the charges inside the closed surface.
Discussion of Gauss law
(i) The total electric flux through the closed surface depends only on the charges enclosed by the surface and the charges present outside the surface will not contribute to the flux and the shape of the closed surface which can be chosen arbitrarily.
(ii) The total electric flux is independent of the location of the charges inside the closed surface.
(iii) To arrive at equation (1.62), we have chosen a spherical surface. This imaginary surface is called a Gaussian surface. The shape of the Gaussian surface to be chosen depends on the type of charge configuration and the kind of symmetry existing in that charge configuration. The electric field is spherically symmetric for a point charge, therefore spherical Gaussian surface is chosen. Cylindrical and planar Gaussian surfaces can be chosen for other kinds of charge configurations.
(iv) In the LHS of equation (1.62), the electric field ![]() is due to charges present inside and outside the Gaussian surface but the charge Qencl denotes the charges which lie only inside the Gaussian surface.
is due to charges present inside and outside the Gaussian surface but the charge Qencl denotes the charges which lie only inside the Gaussian surface.
(v) The Gaussian surface cannot pass through any discrete charge but it can pass through continuous charge distributions. It is because, very close to the discrete charges, the electric field is not well defined.
(vi) Gauss law is another form of Coulomb’s law and it is also applicable to the charges in motion. Because of this reason, Gauss law is treated as much more general law than Coulomb’s law.
EXAMPLE 1.18
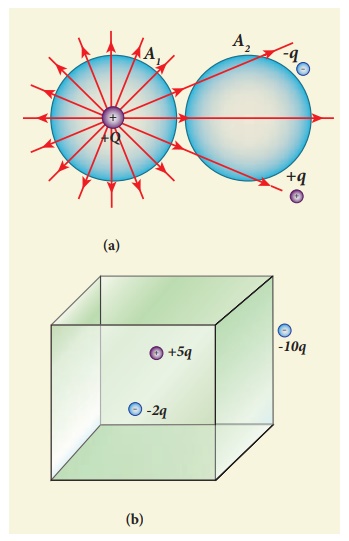
(i) In figure (a), calculate the electric flux through the closed areas A1 and A2.
(ii) In figure (b), calculate the electric flux through the cube
Solution
(i) In figure (a), the area A1 encloses the charge Q. So electric flux through this closed surface A1 is Q/ ε . But the closed surface A2 contains no charges inside, so electric flux through A2 is zero.
(ii) In figure (b), the net charge inside the cube is 3q and the total electric flux in the cube is therefore ΦE = 3q/ ε .
Note that the charge -10 q lies outside the cube and it will not contribute the total flux through the surface of the cube.
Related Topics