Electrostatics - Electric Flux | 12th Physics : Electrostatics
Chapter: 12th Physics : Electrostatics
Electric Flux
Electric
Flux
The number of electric
field lines crossing a given area kept normal to the electric field lines is
called electric flux. It is usually denoted by the Greek letter ΦE and its unit is N m2
C-1. Electric flux is a scalar quantity and it can be positive or
negative. For a simpler understanding of electric flux, the following Figure
1.32 is useful.
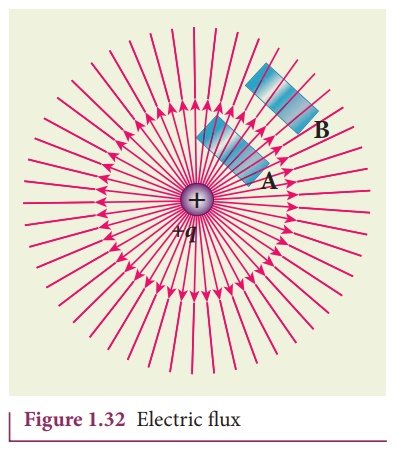
The electric field of a
point charge is drawn in this figure. Consider two small rectangular area
elements placed normal to the field at regions A and B. Even though these
elements have the same area, the number of electric field lines crossing the
element in region A is more than that crossing the element in region B.
Therfore the electric flux in region A is more than that in region B. The
electric field strength for a point charge decreases as the distance increases,
then for a point charge electric flux also decreases as the distance increases.
The above discussion gives a qualitative idea of electric flux. However a
precise definition of electric flux is needed.![]()
![]()
Electric flux for uniform Electric field
Consider a uniform
electric field in a region of space. Let us choose an area A normal to the
electric field lines as shown in Figure 1.33 (a). The electric flux for this
case is

Suppose the same area A
is kept parallel to the uniform electric field, then no electric field lines
pierce through the area A , as shown in Figure 1.33(b). The electric flux for
this case is zero.

If the area is inclined
at an angle θ with the field, then
the component of the electric field perpendicular to the area alone contributes
to the electric flux. The electric field component parallel to the surface area
will not contribute to the electric flux. This is shown in Figure 1.33 (c). For
this case, the electric flux

Further, θ is also the
angle between the electric field and the direction normal to the area. Hence in
general, for uniform electric field, the electric flux is defined as
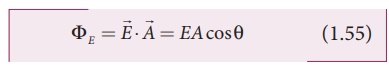
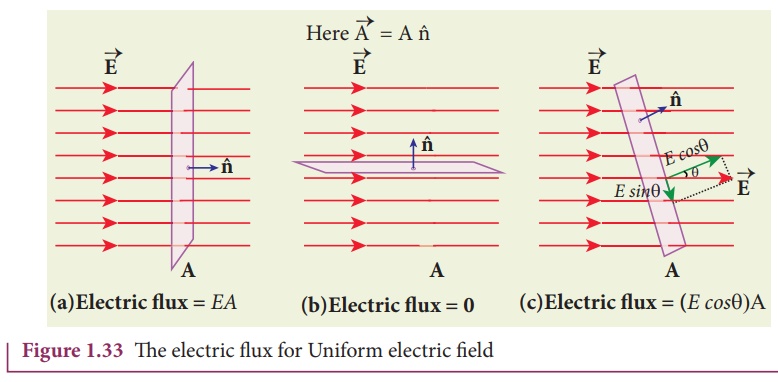
Here, note that ![]() is the area vector
is the area vector ![]() =A
=A![]() . Its magnitude is simply
the area A and the direction is along the unit vector n perpendicular to
the area as shown in Figure
. Its magnitude is simply
the area A and the direction is along the unit vector n perpendicular to
the area as shown in Figure![]() 1.33.Using this definition
for flux, ΦE =
1.33.Using this definition
for flux, ΦE = ![]() ⋅
⋅ ![]() , equations (1.53) and (1.54) can be obtained as special cases.
, equations (1.53) and (1.54) can be obtained as special cases.
In Figure 1.33 (a), θ =
0º so ΦE = ![]() ⋅
⋅ ![]() = EA
= EA
In Figure 1.33 (b), θ =
90 º so ΦE = ![]() ⋅
⋅ ![]() = 0
= 0
EXAMPLE 1.17
Calculate the electric
flux through the rectangle of sides 5 cm and 10 cm kept in the region of a
uniform electric field 100 NC-1. The angle θ is 60o. Suppose θ
becomes zero, what is the electric flux?
Solution
The electric flux
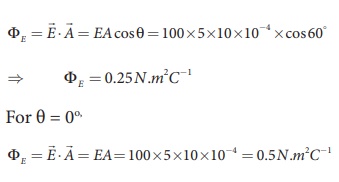
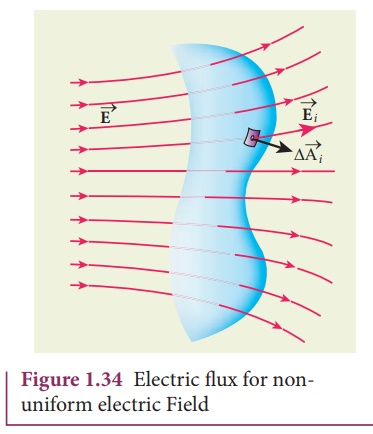
Electric flux in a non uniform electric field and an arbitrarily shaped area
Suppose the electric
field is not uniform and the area A is not flat (Figure 1.34), then the entire
area is divided into n small area segments ∆![]() 1 , ∆
1 , ∆![]() 2 , ∆
2 , ∆![]() 3 ......... ∆
3 ......... ∆![]() n suchthat
each area element is almost flat and the electric field over each area element
is considered to be uniform.
n suchthat
each area element is almost flat and the electric field over each area element
is considered to be uniform.
The electric flux for
the entire area A is approximately written as
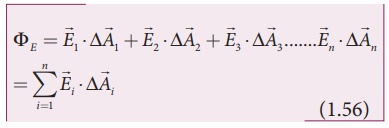
By taking the limit ∆![]() i → 0 (for all i) the summation
in equation (1.56) becomes integration. The total electric flux for the entire
area is given by
i → 0 (for all i) the summation
in equation (1.56) becomes integration. The total electric flux for the entire
area is given by

From Equation (1.57), it
is clear that the electric flux for a given surface depends on both the
electric field pattern on the surface area and orientation of the surface with
respect to the electric field.
Related Topics