Electrostatics - Equi-potential Surface | 12th Physics : Electrostatics
Chapter: 12th Physics : Electrostatics
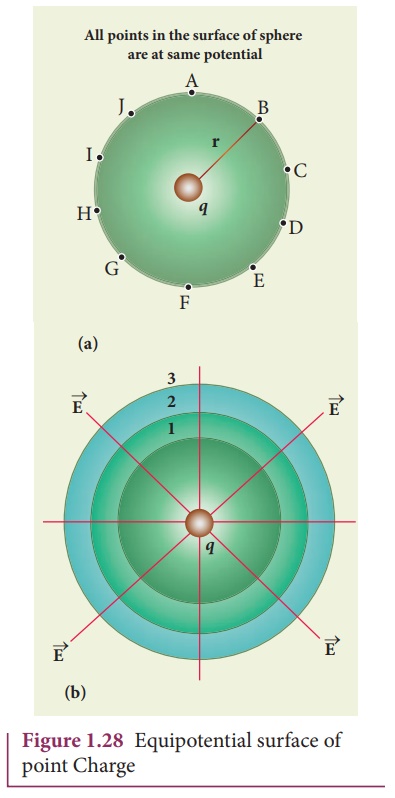
Equi-potential Surface
Equi-potential Surface
Consider a point charge
q located at some point in space and an imaginary sphere of radius r is chosen
by keeping the charge q at its center (Figure 1.28(a)). The electric potential
at all points on the surface of the given sphere is the same. Such a surface is
called an equipotential surface.
An equipotential surface
is a surface on which all the points are at the same potential. For a point charge the
equipotential surfaces are concentric spherical surfaces as shown in Figure
1.28(b). Each spherical surface is an equipotential surface but the value of
the ![]()
![]()
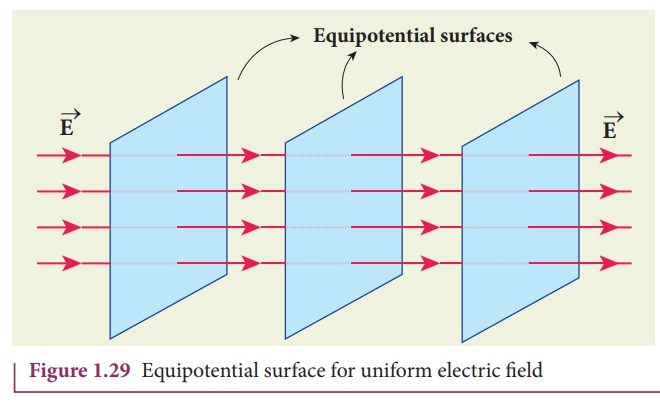
For a uniform electric
field, the equipotential surfaces form a set of planes normal to the electric
field ![]() . This is shown in the Figure 1.29.
. This is shown in the Figure 1.29.
Properties of
equipotential surfaces
(i) The work done to
move a charge q between any two points A and B, W = q (VB ‚Äď VA).
If the points A and B lie on the same equipotential surface, work done is zero
because VA = VB.
(ii) The electric field
is normal to an equipotential surface. If it is not normal, then there is a
component of the field parallel to the surface. Then work must be done to move
a charge between two points on the same surface. This is a contradiction.
Therefore the electric field must always be normal to equipotential surface.
Related Topics