Physics - Electromagnetic Induction and Alternating Current: Exercises and Example Solved Numerical problems | 12th Physics : Electromagnetic Induction and Alternating Current
Chapter: 12th Physics : Electromagnetic Induction and Alternating Current
Electromagnetic Induction and Alternating Current: Exercises and Example Solved Numerical problems
Numerical problems
1. A square coil of side 30 cm with 500 turns is kept in a uniform magnetic field of 0.4 T. The plane of the coil is inclined at an angle of 30o to the field. Calculate the magnetic flux through the coil. (Ans: 9 Wb)

2. A straight metal wire crosses a magnetic field of flux 4 mWb in a time 0.4 s. Find the magnitude of the emf induced in the wire. (Ans: 10 mV)

3. The magnetic flux passing through a coil perpendicular to its plane is a function of time and is given by ╬”B = ( 2t3 + 4t2 + 8t + 8) Wb. If the resistance of the coil is 5 ╬®, determine the induced current through the coil at a time t = 3 second. (Ans: 17.2 A)

4. A closely wound coil of radius 0.02 m is placed perpendicular to the magnetic field. When the magnetic field is changed from 8000 T to 2000 T in 6 s, an emf of 44 V is induced. Calculate the number of turns in the coil. (Ans: 35 turns)

5. A rectangular coil of area 6 cm2 having 3500 turns is kept in a uniform magnetic field of 0.4 T. Initially, the plane of the coil is perpendicular to the field and is then rotated through an angle of 180┬║. If the resistance of the coil is 35 Ōä”, find the amount of charge flowing through the coil. (Ans: 48 ├Ś 10-3 C)

6. An induced current of 2.5 mA flows through a single conductor of resistance 100 Ōä”. Find out the rate at which the magnetic flux is cut by the conductor. (Ans: 250 mWbs-1)

7. A fan of metal blades of length 0.4 m rotates normal to a magnetic field of 4 ├Ś10ŌłÆ3T . If the induced emf between the centre and edge of the blade is 0.02 V, determine the rate of rotation of the blade. (Ans: 9.95 revolutions/second)
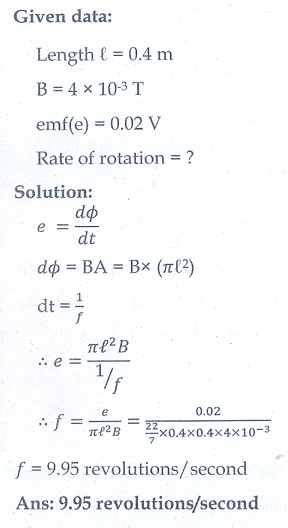
8. A bicycle wheel with metal spokes of 1 m long rotates in EarthŌĆÖs magnetic field. The plane of the wheel is perpendicular to the horizontal component of EarthŌĆÖs field of 4 ├Ś10ŌłÆ5T.If the emf induced across the spokes is 31.4 mV, calculate the rate of revolution of the wheel. (Ans: 250 revolutions/second)
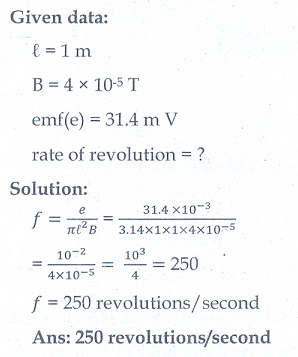
9. Determine the self-inductance of 4000 turn air-core solenoid of length 2m and diameter 0.04 m. (Ans: 12.62 mH)

10. A coil of 200 turns carries a current of 4 A. If the magnetic flux through the coil is 6 x 10-5 Wb, find the magnetic energy stored in the medium surrounding the coil. (Ans: 0.024 J)

11. A 50 cm long solenoid has 400 turns per cm. The diameter of the solenoid is 0.04 m. Find the magnetic flux of a turn when it carries a current of 1 A. (Ans: 1.26 Wb)

12. A coil of 200 turns carries a current of 0.4 A. If the magnetic flux of 4 mWb is linked with the coil, find the inductance
of the coil. (Ans: 2H)

13. Two air core solenoids have the same length of 80 cm and same crossŌĆōsectional area 5 cm2. Find the mutual inductance between them if the number of turns in the first coil is 1200 turns and that in the second coil is 400 turns. (Ans: 0.38 mH)

14. A long solenoid having 400 turns per cm carries a current 2A. A 100 turn coil of cross-sectional area 4 cm2 is placed co-axially inside the solenoid so that the coil is in the field produced by the solenoid. Find the emf induced in the coil if the current through the solenoid reverses its direction in 0.04 sec.
(Ans: 0.20 V)

15. A 200 turn coil of radius 2 cm is placed co-axially within a long solenoid of 3 cm radius. If the turn density of the solenoid is 90 turns per cm, then calculate mutual inductance of the coil.
(Ans: 2.84 mH)

16. The solenoids S1 and S2 are wound on an iron-core of relative permeability 900. The area of their cross-section and their length are the same and are 4 cm2 and 0.04 m respectively. If the number of turns in S1 is 200 and that in S2 is 800, calculate the mutual inductance between the coils. The current in solenoid 1 is increased form 2A to 8A in 0.04 second. Calculate the induced emf in solenoid 2.
(Ans: 1.81H; 271.5 V)

17. A step-down transformer connected to main supply of 220 V is made to operate 11V,88W lamp. Calculate (i) Transformation ratio and (ii) Current in the primary.
(Ans: 1/20 and 0.4A)

18. A 200V/120V step-down transformer of 90% efficiency is connected to an induction stove of resistance 40 Ōä”. Find the current drawn by the primary of the transformer.
(Ans: 2A)

19. The 300 turn primary of a transformer has resistance 0.82 Ōä” and the resistance of its secondary of 1200 turns is 6.2 Ōä”. Find the voltage across the primary if the power output from the secondary at 1600V is 32 kW. Calculate the power losses in both coils when the transformer efficiency is 80%.
(Ans: 8.2 kW and 2.48 kW)

20 . Calculate the instantaneous value at 60o, average value and RMS value of an alternating current whose peak value is 20 A. (Ans: 17.32A, 12.74A, 14.14 A)

Conceptual Questions
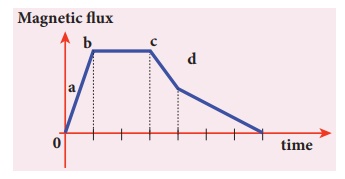
1. A graph between the magnitude of the magnetic flux linked with a closed loop and time is given in the figure. Arrange the regions of the graph in ascending order of the magnitude of induced emf in the loop.

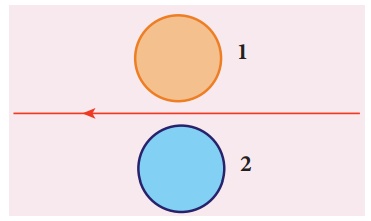
2. Using LenzŌĆÖs law, predict the direction of induced current in conducting rings 1 and 2 when current in the wire is steadily decreasing.

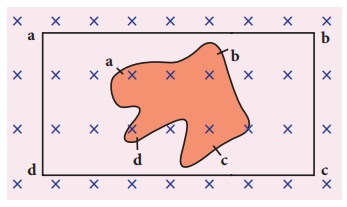
3. A flexible metallic loop abcd in the shape of a square is kept in a magnetic field with its plane perpendicular to the field. The magnetic field is directed into the paper normally. Find the direction of the induced current when the square loop is crushed into an irregular shape as shown in the figure.

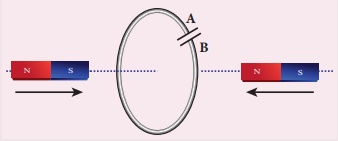
4. Predict the polarity of the capacitor in a closed circular loop when two bar magnets are moved as shown in the figure.

5. In series LC circuit, the voltages across L and C are 180┬░ out of phase. Is it correct? Explain.

6. When does power factor of a series RLC circuit become maximum?

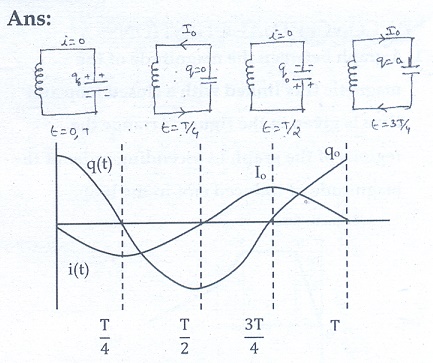
7. Draw graphs showing the distribution of charge in a capacitor and current through an inductor during LC oscillations with respect to time. Assume that the charge in the capacitor is maximum initially.
Electromagnetic Induction: Solved Example Problems
EXAMPLE 4.1
A circular antenna of area 3 m2 is installed at a place in Madurai. The plane of the area of antenna is inclined at 47┬║ with the direction of EarthŌĆÖs magnetic field. If the magnitude of EarthŌĆÖs field at that place is 40773.9 nT find the magnetic flux linked with the antenna.
Solution
B = 40773.9 nT; ╬Ė = 90┬║ ŌĆō 47┬║ = 43┬░;
A = 3m2
We know that ╬”B = BAcos╬Ė

EXAMPLE 4.2
A circular loop of area 5 x 10-2m2 rotates in a uniform magnetic field of 0.2 T. If the loop rotates about its diameter which is perpendicular to the magnetic field as shown in figure. Find the magnetic flux linked with the loop when its plane is (i) normal to the field (ii) inclined 60o to the field and (iii) parallel to the field.
Solution
A = 5 ┬┤ 10-2 m2; B = 0.2 T
(i) ╬Ė = 0┬░
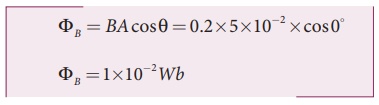
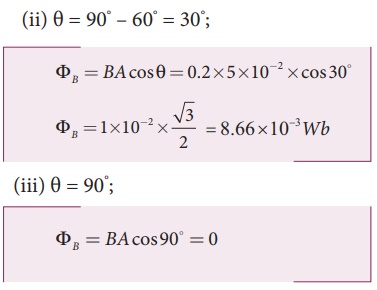
FaradayŌĆÖs Experiments on Electromagnetic Induction: Solved Example Problems
EXAMPLE 4.3
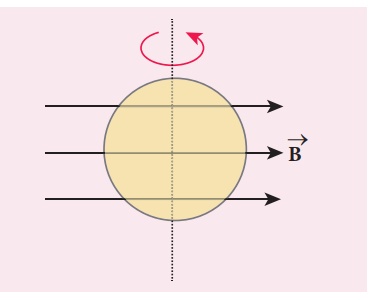
A cylindrical bar magnet is kept along the axis of a circular solenoid. If the magnet is rotated about its axis, find out whether an electric current is induced in the coil.
Solution
The magnetic field of a cylindrical magnet is symmetrical about its axis. As the magnet is rotated along the axis of the solenoid, there is no induced current in the solenoid because the flux linked with the solenoid does not change due to the rotation of the magnet.
EXAMPLE 4.4
A closed coil of 40 turns and of area 200 cm2, is rotated in a magnetic field of flux density 2 Wb m-2. It rotates from a position where its plane makes an angle of 30┬║ with the field to a position perpendicular to the field in a time 0.2 sec. Find the magnitude of the emf induced in the coil due to its rotation.
Solution
N = 40 turns; B = 2 Wb m-2
A = 200 cm2 = 200 ┬┤ 10-4 m2;

EXAMPLE 4.5
A straight conducting wire is dropped horizontally from a certain height with its length along east ŌĆō west direction. Will an emf be induced in it? Justify your answer.
Solution
Yes! An emf will be induced in the wire because it moves perpendicular to the horizontal component of EarthŌĆÖs magnetic field.
FlemingŌĆÖs right hand rule: Solved Example Problems
EXAMPLE 4.6
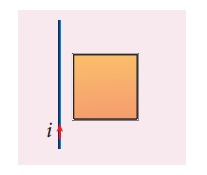
If the current i flowing in the straight conducting wire as shown in the figure decreases, find out the direction of induced current in the metallic square loop placed near it.
Solution
From right hand rule, the magnetic field by the straight wire is directed into the plane of the square loop perpendicularly and its magnetic flux is decreasing. The decrease in flux is opposed by the current induced in the loop by producing a magnetic field in the same direction as the magnetic field of the wire. Again from right hand rule, for this inward magnetic field, the direction of the induced current in the loop is clockwise.
EXAMPLE 4.7
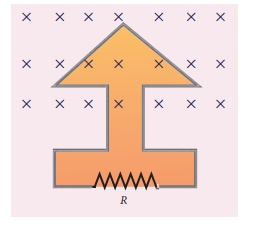
The magnetic flux passes perpendicular to the plane of the circuit and is directed into the paper. If the magnetic flux varies with respect to time as per the following relation: ╬”B = (2t3 +3t2 + 8t +5) mWb , what is the magnitude of the induced emf in the loop when t = 3 s? Find out the direction of current through the circuit.
Solution
╬”B = (2t 3 +3t2 + 8t +5) mWb; N =1; t = 3 s
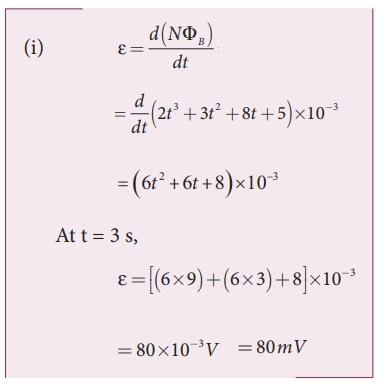
(ii) As time passes, the magnetic flux linked with the loop increases. According to LenzŌĆÖs law, the direction of the induced current should be in a way so as to oppose the flux increase. So, the induced current flows in such a way to produce a magnetic field opposite to the given field. This magnetic field is perpendicularly outwards. Therefore, the induced current flows in anti-clockwise direction.
Motional emf from FaradayŌĆÖs law and Energy conservation: Solved Example Problems
EXAMPLE 4.8
A conducting rod of length 0.5 m falls freely from the top of a building of height 7.2 m at a place in Chennai where the horizontal component of EarthŌĆÖs magnetic field is 40378.7 nT. If the length of the rod is perpendicular to EarthŌĆÖs horizontal magnetic field, find the emf induced across the conductor when the rod is about to touch the ground. [Take g = 10 m s-2]
Solution
l = 0.5 m; h = 7.2 m; u = 0 m s-1;
g = 10 m s-2; BH = 40378.7 nT
The final velocity of the rod is
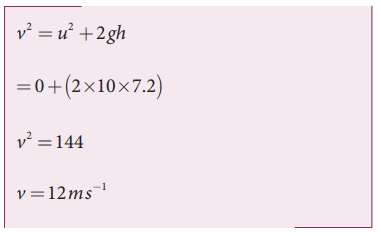
Induced emf when the rod is about to touch the ground, ╬Ą = BH lv
= 40, 378.7 ├Ś10ŌłÆ9 ├Ś 0.5 ├Ś12
=242 .27 ├Ś10ŌłÆ6V
=242 .27┬ĄV
EXAMPLE 4.9
A copper rod of length l rotates about one of its ends with an angular velocity Žē in a magnetic field B as shown in the figure. The plane of rotation is perpendicular to the field. Find the emf induced between the two ends of the rod.
Solution
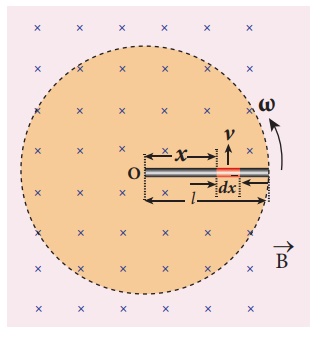
Consider a small element of length dx at a distance x from the centre of the circle described by the rod. As this element moves perpendicular to the field with a linear velocity v = xŽē , the emf developed in the element dx is
d ╬Ą = Bvdx = B( xŽē)dx
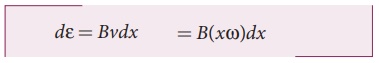
This rod is made up of many such elements, moving perpendicular to the field. The emf developed across two ends is
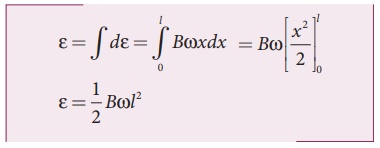
Self-inductance of a long solenoid(Eddy Currents)
EXAMPLE 4.10
A solenoid of 500 turns is wound on an iron core of relative permeability 800. The length and radius of the solenoid are 40 cm and 3 cm respectively. Calculate the average emf induced in the solenoid if the current in it changes from 0 to 3 A in 0.4 second.
Solution
N = 500 turns; ┬Ąr = 800 ;
l = 40 cm = 0.4 m; r = 3 cm = 0.03 m;
di = 3 ŌĆō 0 = 3 A; dt = 0.4 s
Self inductance,

EXAMPLE 4.11
The self-inductance of an air-core solenoid is 4.8 mH. If its core is replaced by iron core, then its self-inductance becomes 1.8 H. Find out the relative permeability of iron.
Solution

Mutual inductance between two long co-axial solenoids(Eddy Curent): Solved Example Problems
EXAMPLE 4.12
The current flowing in the first coil changes from 2 A to 10 A in 0.4 sec. Find the mutual inductance between two coils if an emf of 60 mV is induced in the second coil. Also determine the induced emf in the second coil if the current in the first coil is changed from 4 A to 16 A in 0.03 sec. Consider only the magnitude of induced emf.
Solution
Case (i):
di1 = 10 ŌĆō 2 = 8 A; dt = 0.4 s;
╬Ą2 = 60 ├Ś10ŌłÆ3V
Case (ii):
di1 = 16 ŌĆō 4 = 12 A;
dt = 0.03 s
(i) Mutual inductance of the second coil with respect to the first coil

(ii) Induced emf in the second coil due to the rate of change of current in the first coil is
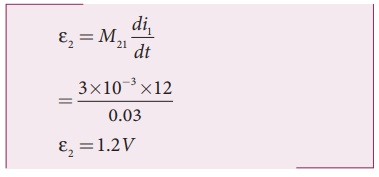
EXAMPLE 4.13
Consider two coplanar, co-axial circular coils A and B as shown in figure. The radius of coil A is 20 cm while that of coil B is 2 cm. The number of turns is 200 and 1000 for coils A and B respectively. Calculate the mutual inductance of coil B with respect to coil A. If the current in coil A changes from 2 A to 6 A in 0.04 sec, determine the induced emf in coil B and the rate of change of flux through the coil B at that instant.
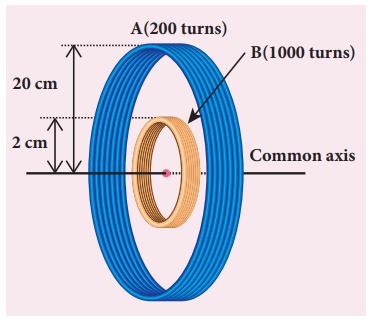
Solution
NA = 200 turns; NB = 1000 turns;
rA = 20 ├Ś 10-2 m; rB = 2 ├Ś 10-2 m;
dt = 0.04 s; diA = 6ŌłÆ2 = 4A
Let iA be the current flowing in coil A, then the magnetic field BA at the centre of the circular coil A is

The rate of change of magnetic flux of coil is

Solved Example Problems on Methods of Producing Induced Emf
Induction of emf by changing the area of the coil: Solved Example Problems
EXAMPLE 4.14
A circular metal of area 0.03 m2 rotates in a uniform magnetic field of 0.4 T. The axis of rotation passes through the centre and perpendicular to its plane and is also parallel to the field. If the disc completes 20 revolutions in one second and the resistance of the disc is 4 Ōä”, calculate the induced emf between the axis and the rim and induced current flowing in the disc.
Solution
A = 0.03 m2; B = 0.4 T; f = 20 rps; R = 4 ╬®

Induction of emf by changing relative orientation of the coil with the magnetic field : Solved Example Problems
EXAMPLE 4.15
A rectangular coil of area 70 cm2 having 600 turns rotates about an axis perpendicular to a magnetic field of 0.4 Wb m-2. If the coil completes 500 revolutions in a minute, calculate the instantaneous emf when the plane of the coil is (i) perpendicular to the field (ii) parallel to the field and (iii) inclined at 60o with the field.
Solution
A = 70 ┬┤ 10-4m2; N = 600 turns
B = 0.4 Wbm-2; f = 500 rpm

Illustration:
An electric power of 2 MW is transmitted to a place through transmission lines of total resistance, say R = 40 ╬®, at two different voltages. One is lower voltage (10 kV) and the other is higher (100 kV). Let us now calculate and compare power losses in these two cases.
Case (i):
P = 2 MW; R = 40 ╬®; V = 10 kV

Case (ii):
P = 2 MW; R = 40 ╬®; V = 100 kV

Thus it is clear that when an electric power is transmitted at higher voltage, the power loss is reduced to a large extent.
EXAMPLE 4.16
An ideal transformer has 460 and 40,000 turns in the primary and secondary coils respectively. Find the voltage developed per turn of the secondary if the transformer is connected to a 230 V AC mains. The secondaryisgiventoaloadofresistance104Ōä”. Calculate the power delivered to the load.
Solution
NP = 460 turns; NS = 40,000 turns
VP = 230 V; RS = 104 Ōä”

EXAMPLE 4.17
An inverter is common electrical device which we use in our homes. When there is no power in our house, inverter gives AC power to run a few electronic appliances like fan or light. An inverter has inbuilt step-up transformer which converts 12ŌĆåV AC to 240 V AC. The primary coil has 100 turns and the inverter delivers 50 mA to the external circuit. Find the number of turns in the secondary and the primary current.
Solution
Vp = 12 V; Vs = 240 V
Is = 50mA; Np = 100 turns

RMS value of AC:
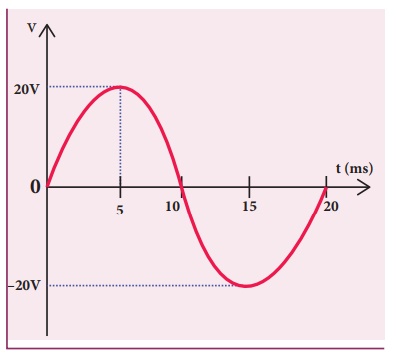
EXAMPLE 4.18
Write down the equation for a sinusoidal voltage of 50 Hz and its peak value is 20 V. Draw the corresponding voltage versus time graph.
Solution

EXAMPLE 4.19
The equation for an alternating current is given by i = 77 sin 314t. Find the peak value, frequency, time period and instantaneous value at t = 2 ms.
Solution
i = 77 sin 314t ; t = 2 ms = 2├Ś10-3 s
The general equation of an alternating current is i = Im sin Žēt . On comparsion,
(i) Peak value, Im = 77 A
(ii) Frequency, f = Žē/2ŽĆ = 314 / 2 ├Ś3.14 = 50 Hz
Time period, T = 1/f = 150 = 0 .02 s
(iv) At t = 2 m s,
Instantaneous value,
i = 77sin(314├Ś2├Ś10ŌłÆ3 )
i = 45.24 A
AC circuit containing only an inductor: Solved Example Problems
EXAMPLE 4.20
A 400 mH coil of negligible resistance is connected to an AC circuit in which an effective current of 6 mA is flowing. Find out the voltage across the coil if the frequency is 1000 Hz.
Solution
L = 400 x 10-3 H; Ieff = 6 x 10-3A
f = 1000 Hz

AC circuit containing only a capacitor: Solved Example Problems
EXAMPLE 4.21
A capacitor of capacitance 102/ŽĆ ┬ĄF is connected across a 220 V, 50 Hz A.C. mains. Calculate the capacitive reactance, RMS value of current and write down the equations of voltage and current.
Solution

Quality factor or QŌĆōfactor: Solved Example Problems
EXAMPLE 4.22
Find the impedance of a series RLC circuit if the inductive reactance, capacitive reactance and resistance are 184 ╬®, 144 ╬® and 30 ╬® respectively. Also calculate the phase angle between voltage and current.
Solution
XL = 184 ╬®; XC = 144 ╬®
R = 30 ╬®
(i ) The impedance is
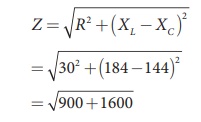
Impedance, Z = 50 Ōä”
(ii) Phase angle is
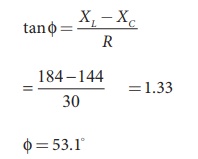
Žå = 53.1
EXAMPLE 4.23
A 500 ╬╝H inductor, 80/ŽĆ2 pF capacitor and a 628 ╬® resistor are connected to form a series RLC circuit. Calculate the resonant frequency and Q-factor of this circuit at resonance.
Solution
L=500├Ś10-6H; C = 80/ŽĆ2 ├Ś10ŌłÆ12 F; R = 628Ōä”
(i) Resonant frequency is

Q =12.5
EXAMPLE 4.24
Find the instantaneous value of alternating voltage Žģ = 10 sin(3 ŽĆ├Ś104 t) volt at i) 0ŌĆås ii) 50 ╬╝s iii) 75 ╬╝s.
Solution
The given equation is Žģ = 10sin (3 ŽĆ├Ś104 t)

EXAMPLE 4.25
The current in an inductive circuit is given by 0.3 sin (200t ŌĆō 40┬░) A. Write the equation for the voltage across it if the inductance is 40 mH.
Solution
L = 40 ├Ś 10-3 H; i = 0.1 sin (200t ŌĆō 40┬║)
XL = ŽēL = 200 ├Ś 40 ├Ś 10-3 = 8 Ōä”
Vm = Im XL = 0.3 ├Ś 8 = 2.4 V
In an inductive circuit, the voltage leads the current by 90o Therefore,
v = Vm sin ( Žēt +90┬║)
v = 2 . 4 sin(200t ŌłÆ40 + 90 ┬║)
v = 2 . 4 sin(200t +50 ┬║)volt
Power in AC Circuits: Solved Example Problems
EXAMPLE 4.26
A series RLC circuit which resonates at 400 kHz has 80 ╬╝H inductor, 2000 pF capacitor and 50 ╬® resistor. Calculate (i) Q-factor of the circuit (ii) the new value of capacitance when the value of inductance is doubled and (iii) the new Q-factor.
Solution
L = 80 ├Ś 10-6H; C = 2000 ├Ś 10-12 F
R = 50 ╬®; fr = 400 ├Ś 103Hz
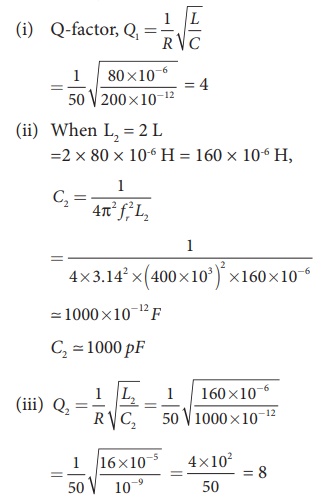
EXAMPLE 4.27
A capacitor of capacitance 10-4 /ŽĆ F, an inductor of inductance 2/ ŽĆ H and a resistor of resistance 100 ╬® are connected to form a series RLC circuit. When an AC supply of 220 V, 50 Hz is applied to the circuit, determine (i) the impedance of the circuit (ii) the peak value of current flowing in the circuit (iii) the power factor of the circuit and (iv) the power factor of the circuit at resonance.
Solution

Related Topics