Motional emf from Lorentz force

Motional emf from Lorentz force

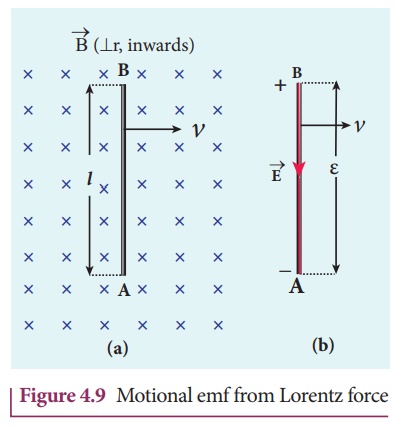
Consider a straight conducting rod AB of length l in a uniform magnetic field  which is directed perpendicularly into the plane of the paper as shown in Figure 4.9(a). The length of the rod is normal to the magnetic field. Let the rod move with a constant velocity  towards right side.

When the rod moves, the free electrons present in it also move with same velocity  in . As a result, the Lorentz force acts on free electrons in the direction from B to A and is given by the relation

The action of this Lorentz force is to accumulate the free electrons at the end A. This accumulation of free electrons produces a potential difference across the rod which in turn establishes an electric field  directed along BA (Figure 4.9(b)). Due to the electric field , the coulomb force starts acting on the free electrons along AB and is given by

The magnitude of the electric field  keeps on increasing as long as accumulation of electrons at the end A continues. The force _E also increases until equilibrium is reached. At equilibrium, the magnetic Lorentz force _B and the coulomb force _E balance each other and no further accumulation of free electrons at the end A takes place.

The potential difference between two ends of the rod is

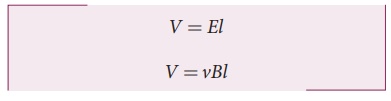
Thus the Lorentz force on the free electrons is responsible to maintain this potential difference and hence produces an emf

As this emf is produced due to the movement of the rod, it is often called as motional emf. If the ends A and B are connected by an external circuit of total resistance R, then current 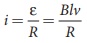 flows in it. The direction of the current is found from right-hand thumb rule.