AC circuit containing a resistor, an inductor and a capacitor in series - Series RLC circuit

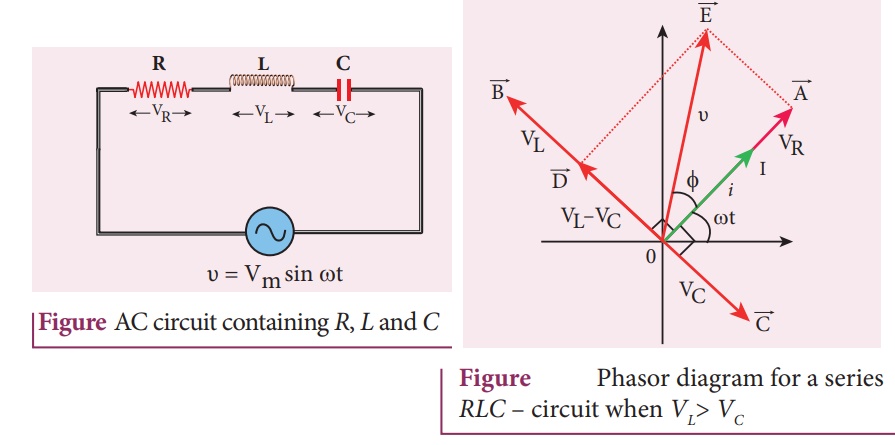
AC circuit containing a resistor, an inductor and a capacitor in series - Series RLC circuit

Consider a circuit containing a resistor of resistance R, a inductor of inductance L and a capacitor of capacitance C connected across an alternating voltage source (Figure 4.51). The applied alternating voltage is given by the equation.

Let i be the resulting circuit current in the circuit at that instant. As a result, the voltage is developed across R, L and C. We know that voltage across R (V_R) is in phase with i, voltage across L (V_L) leads i by π/2 and voltage across C (V_C) lags i by π/2.

The phasor diagram is drawn with current as the reference phasor. The current is represented by the phasor  

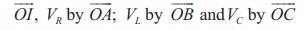 as shown in Figure 4.52.

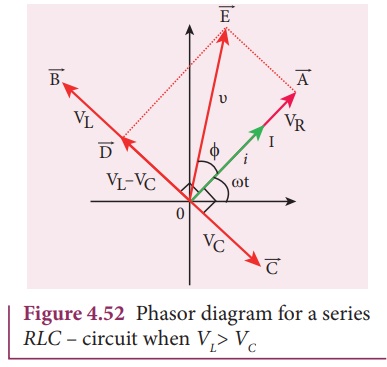
The length of these phasors are

OI = I_m, OA = I_mR, OB = I_mX_L; OC = I_mX_C

The circuit is either effectively inductive or capacitive or resistive that depends on the value of V_L or V_C. Let us assume that V_L > V_C so that net voltage drop across L-C combination is V_L – V_C which is represented by a phasor .

By parallelogram law, the diagonal  gives the resultant voltage Ï… of V_R and (V_L – V_C) and its length OE is equal to V_m. Therefore,

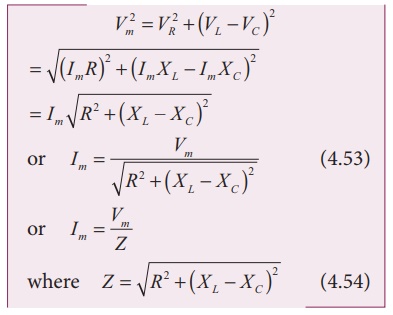
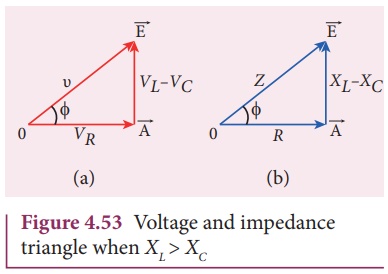
Z is called impedance of the circuit which refers to the effective opposition to the circuit current by the series RLC circuit. The voltage triangle and impedance triangle are given in the Figure 4.53.

From phasor diagram, the phase angle between Ï… and i is found out from the following relation

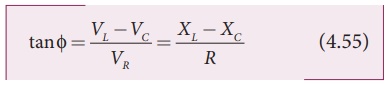
Special cases

(i) If X_L > X_C, (X_L−X_C) is positive and phase angle ϕ is also positive. It means that the applied voltage leads the current by ϕ (or current lags behind voltage by ϕ). The circuit is inductive.

∴ υ = V_m sin ωt; i = I _m sin( ω t −φ)

(ii) If X_L < X_C, (X_L − X_C) is negative and ϕ is also negative. Therefore current leads voltage by ϕ and the circuit is capacitive.

∴ Ï… = V_m sin ωt;  i = I _m sin( ω t + φ)

(iii) If X_L = X_C, Ï• is zero. Therefore current and voltage are in the same phase and the circuit is resistive.

∴ Ï… =V_m sin ωt;   i = I_m sin ωt