Methods of Producing Induced Emf

METHODS OF PRODUCING INDUCED EMF

Introduction

Electromotive force is the characteristic of any energy source capable of driving electric charge around a circuit. We have already learnt that it is not actually a force. It is the work done in moving unit electric charge around the circuit. It is measured in J C^-1 or volt.

Some examples of energy source which provide emf are electrochemical cells, thermoelectric devices, solar cells and electrical generators. Of these, electrical generators are most powerful machines. They are used for large scale power generation.

According to Faraday’s law of electromagnetic induction, an emf is induced in a circuit when magnetic flux linked with it changes. This emf is called induced emf. The magnitude of the induced emf is given by

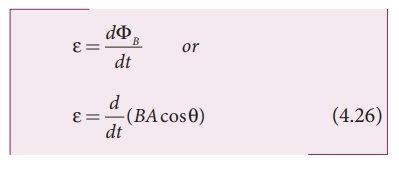
From the above equation, it is clear that induced emf can be produced by changing magnetic flux in any of the following ways.

i.            By changing the magnetic field B

ii.            By changing the area A of the coil and

iii.            By changing the relative orientation θ of the coil with magnetic field

1. Induction of emf by changing the magnetic field

From Faraday’s experiments on electromagnetic induction, it was discovered that an emf is induced in a circuit on changing the magnetic flux of the field through it. The change in flux is brought about by (i) relative motion between the circuit and the magnet (First experiment) variation in current flowing through the nearby coil (Second experiment).

2. Induction of emf by changing the area of the coil

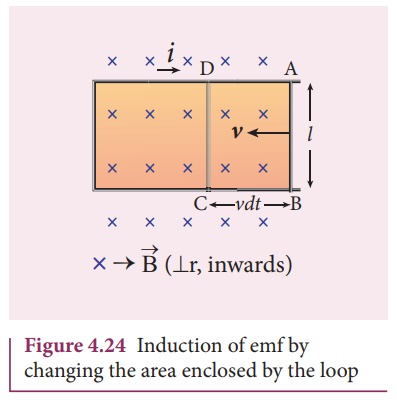
Consider a conducting rod of length l moving with a velocity v towards left on a rectangular metallic framework as shown in Figure 4.24. The whole arrangement is placed in a uniform magnetic field  whose magnetic lines are perpendicularly directed into the plane of the paper.

As the rod moves from AB to DC in a time dt, the area enclosed by the loop and hence the magnetic flux through the loop decreases.

The change in magnetic flux in time dt is

As a result of change in flux, an emf is generated in the loop. The magnitude of the induced emf is

This emf is called motional emf. The direction of induced current is found to be clockwise from Fleming’s right hand rule.

EXAMPLE 4.14

A circular metal of area 0.03 m² rotates in a uniform magnetic field of 0.4 T. The axis of rotation passes through the centre and perpendicular to its plane and is also parallel to the field. If the disc completes 20 revolutions in one second and the resistance of the disc is 4 Ω, calculate the induced emf between the axis and the rim and induced current flowing in the disc.

Solution

A = 0.03 m²; B = 0.4 T; f = 20 rps; R = 4 Ω

3. Induction of emf by changing relative orientation of the coil with the magnetic field

Consider a rectangular coil of N turns kept in a uniform magnetic field  as shown in Figure 4.25(a). The coil rotates in anti-clockwise direction with an angular velocity about an axis, perpendicular to the field.

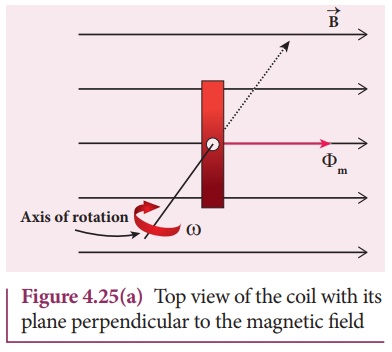
At time = 0, the plane of the coil is perpendicular to the field and the flux linked with the coil has its maximum value Ф_m = BA (where A is the area of the coil).

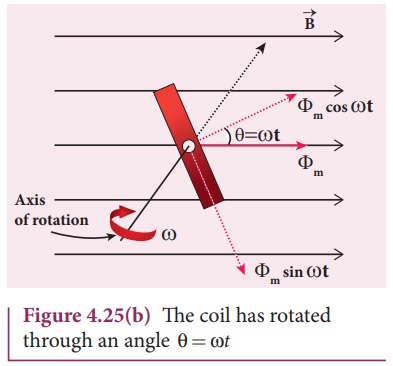
In a time t seconds, the coil is rotated through an angle θ (= ωt) in anti–clockwise direction. In this position, the flux linked is Ф_m cos ωt, a component of Ф_m normal to the plane of the coil (Figure 4.25(b)). The component parallel to the plane (Ф_m sin ωt) has no role in electromagnetic induction.

Therefore, the flux linkage at this deflected position is

According to Faraday’s law, the emf induced at that instant is

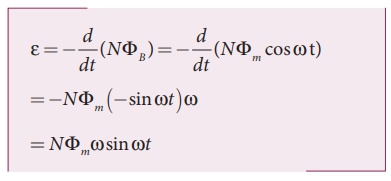
When the coil is rotated through 90o from initial position, sin ωt = 1. Then the maximum value of induced emf is

Therefore, the value of induced emf at that instant is then given by

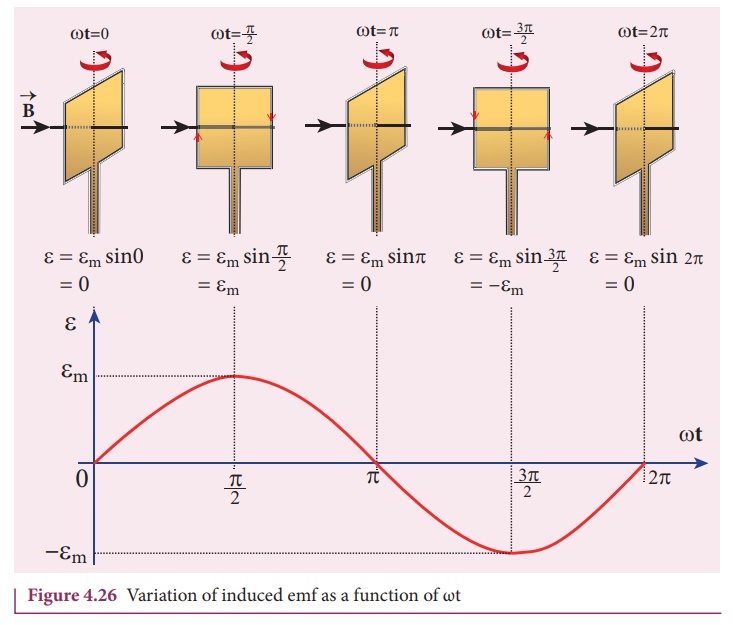
It is seen that the induced emf varies as sine function of the time angle ωt. The graph between induced emf and time angle for one rotation of coil will be a sine curve (Figure 4.26) and the emf varying in this manner is called sinusoidal emf or alternating emf.

If this alternating voltage is given to a closed circuit, a sinusoidally varying current flows in it. This current is called alternating current and is given by

where  I_m is  the  maximum  value  of induced current.

EXAMPLE 4.15

A rectangular coil of area 70 cm2 having 600 turns rotates about an axis perpendicular to a magnetic field of 0.4 Wb m^-2. If the coil completes 500 revolutions in a minute, calculate the instantaneous emf when the plane of the coil is (i) perpendicular to the field (ii) parallel to the field and (iii) inclined at 60o with the field.

Solution

A = 70 ´ 10^-4m₂; N = 600 turns

B = 0.4 Wbm^-2; f = 500 rpm