Chapter: 12th Physics : Electromagnetic Induction and Alternating Current
Electromagnetic Induction: Solved Example Problems
Electromagnetic Induction: Solved Example Problems
EXAMPLE 4.1
A circular antenna of area 3 m2 is installed at a place in Madurai. The plane of the area of antenna is inclined at 47┬║ with the direction of EarthŌĆÖs magnetic field. If the magnitude of EarthŌĆÖs field at that place is 40773.9 nT find the magnetic flux linked with the antenna.
Solution
B = 40773.9 nT; ╬Ė = 90┬║ ŌĆō 47┬║ = 43┬░;
A = 3m2
We know that ╬”B = BAcos╬Ė

EXAMPLE 4.2
A circular loop of area 5 x 10-2m2 rotates in a uniform magnetic field of 0.2 T. If the loop rotates about its diameter which is perpendicular to the magnetic field as shown in figure. Find the magnetic flux linked with the loop when its plane is (i) normal to the field (ii) inclined 60o to the field and (iii) parallel to the field.
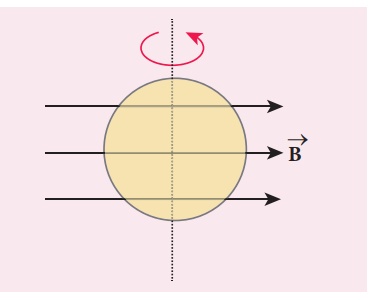
Solution
A = 5 ┬┤ 10-2 m2; B = 0.2 T
(i) ╬Ė = 0┬░
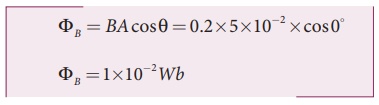
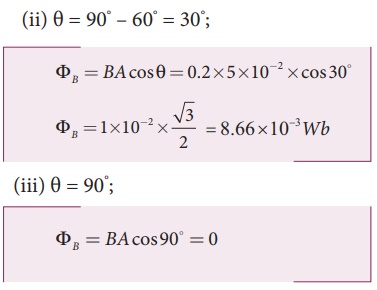
FaradayŌĆÖs Experiments on Electromagnetic Induction: Solved Example Problems
EXAMPLE 4.3
A cylindrical bar magnet is kept along the axis of a circular solenoid. If the magnet is rotated about its axis, find out whether an electric current is induced in the coil.
Solution
The magnetic field of a cylindrical magnet is symmetrical about its axis. As the magnet is rotated along the axis of the solenoid, there is no induced current in the solenoid because the flux linked with the solenoid does not change due to the rotation of the magnet.
EXAMPLE 4.4
A closed coil of 40 turns and of area 200 cm2, is rotated in a magnetic field of flux density 2 Wb m-2. It rotates from a position where its plane makes an angle of 30┬║ with the field to a position perpendicular to the field in a time 0.2 sec. Find the magnitude of the emf induced in the coil due to its rotation.
Solution
N = 40 turns; B = 2 Wb m-2
A = 200 cm2 = 200 ┬┤ 10-4 m2;

EXAMPLE 4.5
A straight conducting wire is dropped horizontally from a certain height with its length along east ŌĆō west direction. Will an emf be induced in it? Justify your answer.
Solution
Yes! An emf will be induced in the wire because it moves perpendicular to the horizontal component of EarthŌĆÖs magnetic field.
FlemingŌĆÖs right hand rule: Solved Example Problems
EXAMPLE 4.6
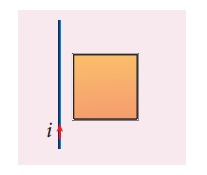
If the current i flowing in the straight conducting wire as shown in the figure decreases, find out the direction of induced current in the metallic square loop placed near it.
Solution
From right hand rule, the magnetic field by the straight wire is directed into the plane of the square loop perpendicularly and its magnetic flux is decreasing. The decrease in flux is opposed by the current induced in the loop by producing a magnetic field in the same direction as the magnetic field of the wire. Again from right hand rule, for this inward magnetic field, the direction of the induced current in the loop is clockwise.
EXAMPLE 4.7
The magnetic flux passes perpendicular to the plane of the circuit and is directed into the paper. If the magnetic flux varies with respect to time as per the following relation: ╬”B = (2t3 +3t2 + 8t +5) mWb , what is the magnitude of the induced emf in the loop when t = 3 s? Find out the direction of current through the circuit.
Solution
╬”B = (2t 3 +3t2 + 8t +5) mWb; N =1; t = 3 s
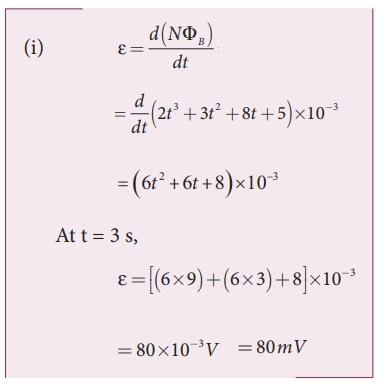
(ii) As time passes, the magnetic flux linked with the loop increases. According to LenzŌĆÖs law, the direction of the induced current should be in a way so as to oppose the flux increase. So, the induced current flows in such a way to produce a magnetic field opposite to the given field. This magnetic field is perpendicularly outwards. Therefore, the induced current flows in anti-clockwise direction.
Motional emf from FaradayŌĆÖs law and Energy conservation: Solved Example Problems
EXAMPLE 4.8
A conducting rod of length 0.5 m falls freely from the top of a building of height 7.2 m at a place in Chennai where the horizontal component of EarthŌĆÖs magnetic field is 40378.7 nT. If the length of the rod is perpendicular to EarthŌĆÖs horizontal magnetic field, find the emf induced across the conductor when the rod is about to touch the ground. [Take g = 10 m s-2]
Solution
l = 0.5 m; h = 7.2 m; u = 0 m s-1;
g = 10 m s-2; BH = 40378.7 nT
The final velocity of the rod is
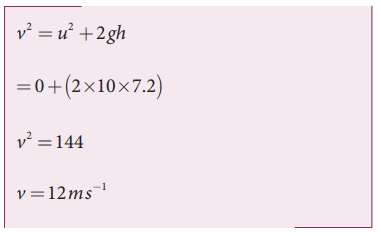
Induced emf when the rod is about to touch the ground, ╬Ą = BH lv
= 40, 378.7 ├Ś10ŌłÆ9 ├Ś 0.5 ├Ś12
=242 .27 ├Ś10ŌłÆ6V
=242 .27┬ĄV
EXAMPLE 4.9
A copper rod of length l rotates about one of its ends with an angular velocity Žē in a magnetic field B as shown in the figure. The plane of rotation is perpendicular to the field. Find the emf induced between the two ends of the rod.
Solution
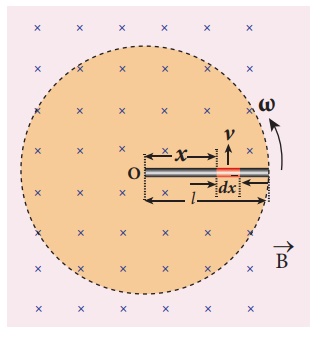
Consider a small element of length dx at a distance x from the centre of the circle described by the rod. As this element moves perpendicular to the field with a linear velocity v = xŽē , the emf developed in the element dx is
d ╬Ą = Bvdx = B( xŽē)dx
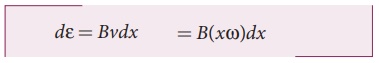
This rod is made up of many such elements, moving perpendicular to the field. The emf developed across two ends is
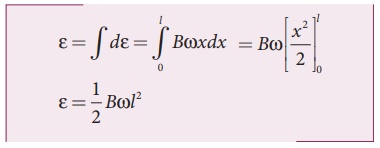
Related Topics