Self-inductance of a long solenoid

Self-inductance of a long solenoid

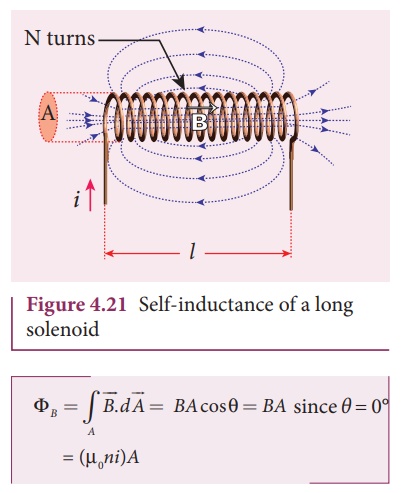
Consider a long solenoid of length l and cross-sectional area A. Let n be the number of turns per unit length (or turn density) of the solenoid. When an electric current i is passed through the solenoid, a magnetic field is produced by it which is almost uniform and is directed along the axis of the solenold as shown in Figure 4.21. The magnetic field at any point inside the solenoid is given by (Refer section 3.9.3)

B = µ ni

As this magnetic field passes through the solenoid, the windings of the solenoid are linked by the field lines. The magnetic flux passing through each turn is

The total magnetic flux linked or flux linkage of the solenoid with N turns (the total number of turns N is given by N = n l) is

Comparing equations (4.15) and (4.17), we have

From the above equation, it is clear that inductance depends on the geometry of the solenoid (turn density n, cross-sectional area A, length l) and the medium present inside the solenoid. If the solenoid is filled with a dielectric medium of relative permeability µ_r , then

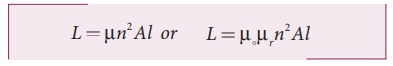
Energy stored in an inductor

Whenever a current is established in the circuit, the inductance opposes the growth of the current. In order to establish a current in the circuit, work is done against this opposition by some external agency. This work done is stored as magnetic potential energy.

Let us assume that electrical resistance of the inductor is negligible and inductor effect alone is considered. The induced emf ε at any instant t is

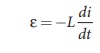
Let dW be work done in moving a charge dq in a time dt against the opposition, then

Total work done in establishing the current i is

This work done is stored as magnetic potential energy.

The energy density is the energy stored per unit volume of the space and is given by

EXAMPLE 4.10

A solenoid of 500 turns is wound on an iron core of relative permeability 800. The length and radius of the solenoid are 40 cm and 3 cm respectively. Calculate the average emf induced in the solenoid if the current in it changes from 0 to 3 A in 0.4 second.

Solution

N = 500 turns; µ_r = 800 ;

l = 40 cm = 0.4 m; r = 3 cm = 0.03 m;

di = 3 – 0 = 3 A; dt = 0.4 s

Self inductance,

EXAMPLE 4.11

The self-inductance of an air-core solenoid is 4.8 mH. If its core is replaced by iron core, then its self-inductance becomes 1.8 H. Find out the relative permeability of iron.

Solution