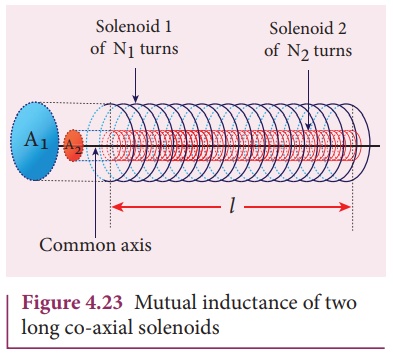
Mutual inductance between two long co-axial solenoids

Mutual inductance between two long co-axial solenoids

Consider two long co-axial solenoids of same length l. The length of these solenoids is large when compared to their radii so that the magnetic field produced inside the solenoids is uniform and the fringing effect at the ends may be ignored. Let A₁ and A₂ be the area of cross section of the solenoids with A₁ being greater than A₂ as shown in Figure 4.23. The turn density of these solenoids are n₁ and n₂ respectively.

Let i₁ be the current flowing through solenoid 1, then the magnetic field produced inside it is

As the field lines of ₁ are passing through the area bounded by solenoid 2, the magnetic flux is linked with each turn of solenoid 2 due to solenoid 1 and is given by

The flux linkage of solenoid 2 with total turns N₂ is

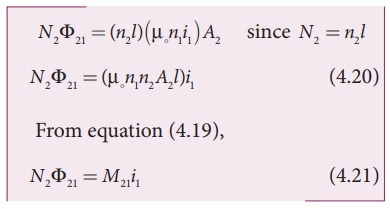
Comparing the equations (4.20) and (4.21),

This gives the expression for mutual inductance M₂₁ of the solenoid 2 with respect to solenoid 1. Similarly, we can find mutual inductance M₁₂ of solenoid 1 with respect to solenoid 2 as given below.

The magnetic field produced by the solenoid 2 when carrying a current i₂ is

B₂ = µ n₂i₂

This magnetic field B₂ is uniform inside the solenoid 2 but outside the solenoid 2, it is almost zero. Therefore for solenoid 1, the area A₂ is the effective area over which the magnetic field B₂ is present; not area A₁. Then the magnetic flux Φ₁₂ linked with each turn of solenoid 1 due to solenoid 2 is

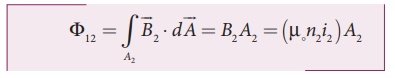
The flux linkage of solenoid 1 with total turns N₁ is

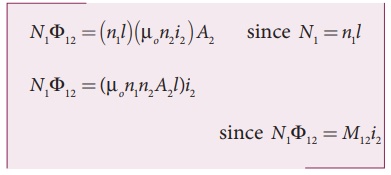
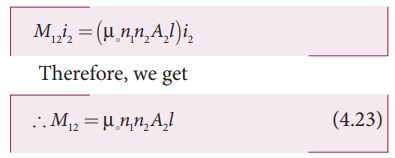
From equation (4.22) and (4.23), we can write

In general, the mutual inductance between two long co-axial solenoids is given by

If a dielectric medium of relative permeability µ_r is present inside the solenoids, then

M  = µ n₁ n₂ A₂ l

(or) M = µ µ_r n₁ n₂ A₂ l

EXAMPLE 4.12

The current flowing in the first coil changes from 2 A to 10 A in 0.4 sec. Find the mutual inductance between two coils if an emf of 60 mV is induced in the second coil. Also determine the induced emf in the second coil if the current in the first coil is changed from 4 A to 16 A in 0.03 sec. Consider only the magnitude of induced emf.

Solution

Case (i):

di₁ = 10 – 2 = 8 A; dt = 0.4 s;

ε₂ = 60 ×10^−3V

Case (ii):

di₁ = 16 – 4 = 12 A;

dt = 0.03 s

(i) Mutual inductance of the second coil with respect to the first coil

(ii) Induced emf in the second coil due to the rate of change of current in the first coil is

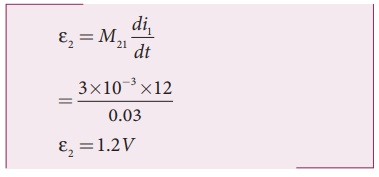
EXAMPLE 4.13

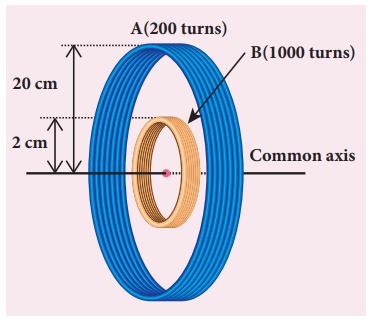
Consider two coplanar, co-axial circular coils A and B as shown in figure. The radius of coil A is 20 cm while that of coil B is 2 cm. The number of turns is 200 and 1000 for coils A and B respectively. Calculate the mutual inductance of coil B with respect to coil A. If the current in coil A changes from 2 A to 6 A in 0.04 sec, determine the induced emf in coil B and the rate of change of flux through the coil B at that instant.

Solution

N_A = 200 turns; N_B = 1000 turns;

r_A = 20 × 10^-2 m; r_B = 2 × 10^-2 m;

dt = 0.04 s; di_A = 6−2 = 4A

Let i_A be the current flowing in coil A, then the magnetic field B_A at the centre of the circular coil A is

The rate of change of magnetic flux of coil is