Introduction, Definition, Formula, Physical significance | Electromagnetic Induction - Eddy Currents | 12th Physics : Electromagnetic Induction and Alternating Current
Chapter: 12th Physics : Electromagnetic Induction and Alternating Current
Eddy Currents
SELF-INDUCTION
Introduction
Inductor is a device
used to store energy in a magnetic field when an electric current flows through
it. The typical examples are coils, solenoids and toroids shown in Figure 4.18.
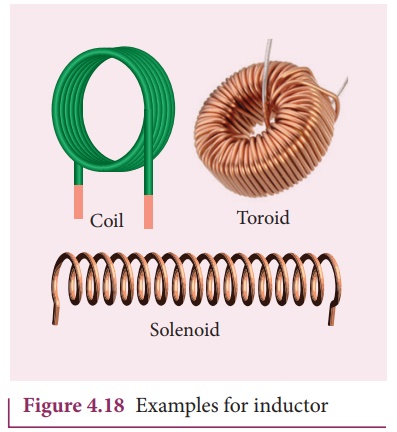
Inductance is the property of inductors to generate emf due to the change in current flowing through that circuit (self-induction) or a change in current through a neighbouring circuit with which it is magnetically linked (mutual induction). We will study about self-induction and mutual induction in the next sections.
Self-induction
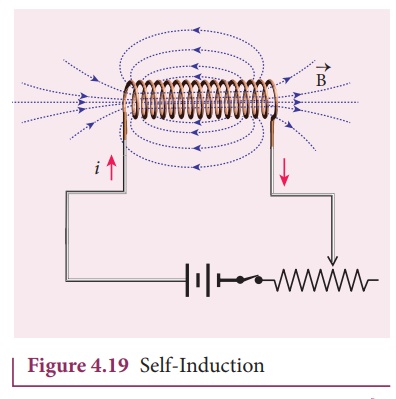
An electric current
flowing through a coil will set up a magnetic field around it. Therefore, the
magnetic flux of the magnetic field is linked with that coil itself. If this
flux is changed by changing the current, an emf is induced in that same coil
(Figure 4.19). This phenomenon is known as self-induction. The emf induced is
called self-induced emf.
Let ΦB
be the magnetic flux linked with each turn of the coil of N turns, then the
total flux linked with the coil NΦB (flux linkage) is
proportional to the current i in the coil.
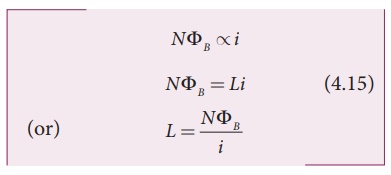
The constant of
proportionality L is called self-inductance of the coil. It is also
referred to as the coefficient of self-induction. If i =1A , then L
= NΦB
. Self-inductance or simply inductance of a coil is defined as the flux
linkage of the coil when 1A current flows through it.
When the current i
changes with time, an emf is induced in it. From Faraday’s law of
electromagnetic induction, this self-induced emf is given by
The negative sign in the
above equation means that the self-induced emf always opposes the change in
current with respect to time. If di/dt =1 A s−1 , then L =−ε .
Inductance of a coil is
also defined as the opposing emf induced in the coil when the rate of change of
current through the coil is 1 A s−1.
Unit of inductance
Inductance is a scalar
and its unit is Wb A-1 or V s A-1 . It is also measured in henry (H).
H = 1 W b A− 1 =1 V s A−1
The dimensional formula
of inductance is M L2 T - 2 A-2 .
If i = 1 A and N
ΦB =1 Wb turns, then =1H .
Therefore, the
inductance of the coil is said to be one henry if a current of 1 A
produces unit flux linkage in the coil.
If di/dt = 1 As− 1 and ε =−1 V , then L H =1 .
Therefore, the
inductance of the coil is one henry if a current changing at the rate of
1 A s−1 induces an opposing emf of 1 V in it.
Physical significance of inductance
We have learnt about
inertia in XI standard. In translational motion, mass is a measure of inertia;
in the same way, for rotational motion, moment of inertia is a measure of
rotational inertia (Refer sections 3.2.1 and 5.4 of XI physics text book).
Generally, inertia means opposition to change its state.
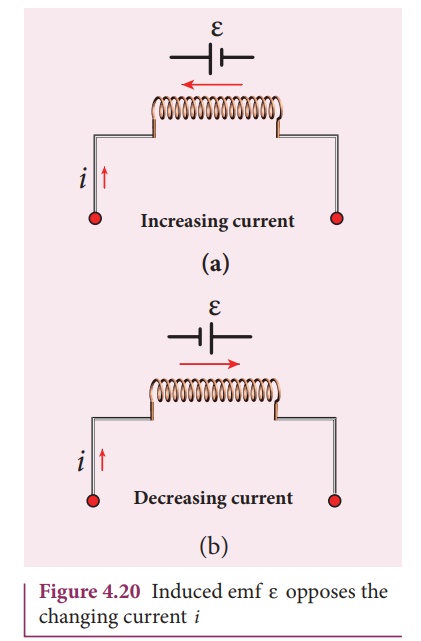
The inductance plays the
same role in a circuit as mass and moment of inertia play in mechanical motion.
When a circuit is switched on, the increasing current induces an emf which
opposes the growth of current in a circuit (Figure 4.20(a)). Likewise, when
circuit is broken, the decreasing current induces an emf in the reverse
direction. This emf now opposes the decay of current (Figure 4.20(b)).
Thus, inductance of the
coil opposes any change in current and tries to maintain the original state.
Related Topics