Power In AC Circuits

POWER IN AC CIRCUITS

1. Introduction of power in AC circuits

Power of a circuit is defined as the rate of consumption of electric energy in that circuit. It is given by the product of the voltage and current. In an AC circuit, the voltage and current vary continuously with time. Let us first calculate the power at an instant and then it is averaged over a complete cycle.

The alternating voltage and alternating current in the series RLC circuit at an instant are given by

v=V_m sin ωt   and  i = I _m sin( ω t + φ)

where Ï• is the phase angle between Ï… and i. The instantaneous power is then written as

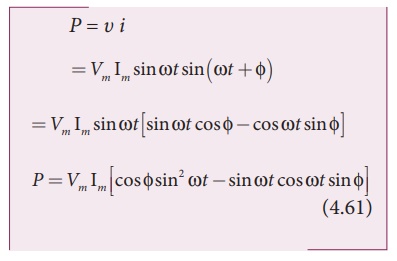
Here the average of sin2 Ï‰t over a cycle is 1/2 and that of sin ω t cos ωt is zero. Substituting these values, we obtain average power over a cycle.

where V_RMS I_RMS is called apparent power and cos Ï• is power factor. The averagezpower of an AC circuit is also known as the true power of the circuit.

Special Cases

(i) For a purely resistive circuit, the phase angle between voltage and current is zero and cos Ï• = 1.

∴ P_av = V_RMS  I_RMS

(ii) For a purely inductive or capacitive circuit, the phase angle is ± π/2 and cos(± π/2)=0.

∴  P_av = 0

(iii)    For series RLC circuit, the phase angle

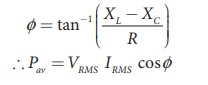
(iv) For series RLC circuit at resonance,  the phase angle is zero and cos . Ï• =1

∴ P_av =  V_RMS I_RMS

2. Wattless current

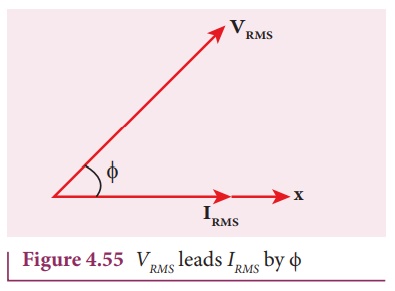
Consider an AC circuit in which there is a phase angle of Ï• between V_RMS and I_RMS and voltage is assumed to be leading the current by Ï• as shown in the phasor diagram (Figure 4.55).

Now, I_RMS is resolved into two perpendicular components namely, I_RMS cos φ along V_RMS and I_RMS sin φ perpendicular to V_RMS as shown in Figure 4.56.

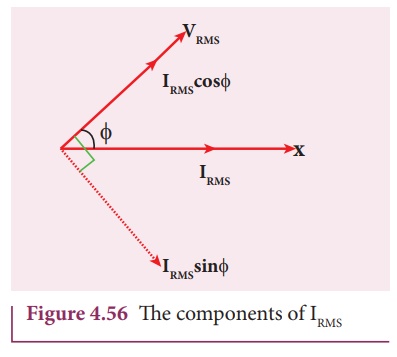
(i) The component of current ( I _RMS cos φ) which is in phase with the voltage is called active component. The power consumed by this current V_RMS I_RMS cos φ . So that it is also known as ‘Wattful’ current.

(ii) The other component ( I _RMS sin φ) which has a phase angle of Ï€/2  with the voltage is called reactive component. The power consumed is zero. So that it is also known as ‘Wattless’ current.

The current in an AC circuit is said to be wattless current if the power consumed by it is zero. This wattless current happens in a purely inductive or capacitive circuit.

3. Power factor

The power factor of a circuit is defined in one of the following ways:

(i) Power factor = cos Ï• = cosine of the angle of lead or lag

(ii) Power factor = R/Z = Impedance / Resistance

(iii) Power factor = VI cos φ / VI

 = True power / Apparent power

Some examples for power factors:

(i) Power factor = cos 0° = 1 for a pure resistive circuit because the phase angle ϕ between voltage and current is zero.

(ii) Power factor = cos(±π /2 )= 0 for a purely inductive or capacitive circuit because the phase angle ϕ between voltage and current is ±π /2 .

(iii) Power factor lies between 0 and 1 for a circuit having R, L and C in varying proportions.

4. Advantages and disadvantages of AC over DC

There are many advantages and disadvantages of AC system over DC system.

Advantages:

(i) The generation of AC is cheaper than that of DC.

(ii) When AC is supplied at higher voltages, the transmission losses are small compared to DC transmission.

(iii) AC can easily be converted into DC with the help of rectifiers.

Disadvantages:

(i) Alternating voltages cannot be used for certain applications e.g. charging of batteries, electroplating, electric traction etc.

(ii) At high voltages, it is more dangerous to work with AC than DC.

EXAMPLE 4.26

A series RLC circuit which resonates at 400 kHz has 80 μH inductor, 2000 pF capacitor and 50 Ω resistor. Calculate (i) Q-factor of the circuit (ii) the new value of capacitance when the value of inductance is doubled and (iii) the new Q-factor.

Solution

L = 80 × 10^-6H; C = 2000 × 10^-12 F

R = 50 Ω; f_r = 400 × 10³Hz

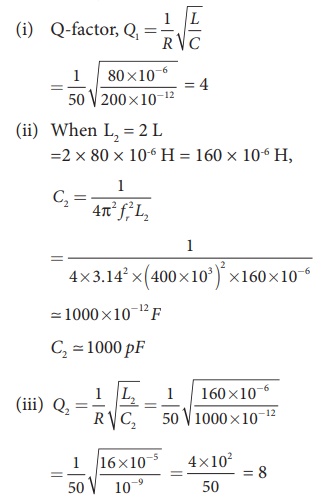
EXAMPLE 4.27

A capacitor of capacitance 10^-4 /π F, an inductor of inductance 2/ π H and a resistor of resistance 100 Ω are connected to form a series RLC circuit. When an AC supply of 220 V, 50 Hz is applied to the circuit, determine (i) the impedance of the circuit (ii) the peak value of current flowing in the circuit (iii) the power factor of the circuit and (iv) the power factor of the circuit at resonance.

Solution