Mutual induction

Mutual induction

When an electric current passing through a coil changes with time, an emf is induced in the neighbouring coil. This phenomenon is known as mutual induction and the emf is called mutually induced emf.

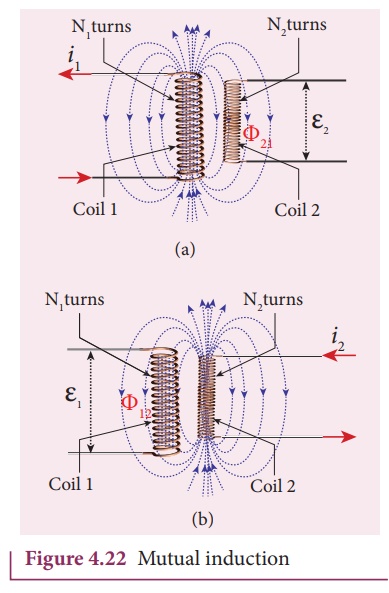
Consider two coils which are placed close to each other. If an electric current i₁ is sent through coil 1, the magnetic field produced by it is also linked with coil 2 as shown in Figure 4.22(a).

Let Φ₂₁ be the magnetic flux linked with each turn of the coil 2 of N₂ turns due to coil 1, then the total flux linked with coil 2 ( N₂ Φ ₂₁ ) is proportional to the current i₁ in the coil 1.

The constant of proportionality M₂₁ is the mutual inductance of the coil 2 with respect to coil 1. It is also called as coefficient of mutual induction. If i₁ =1A , then M ₂₁ = N₂ Φ ₂₁ . Therefore, the mutual inductance M₂₁ is defined as the flux linkage of the coil 2 when 1A current flows through coil 1.

When the current i₁ changes with time, an emf ε₂ is induced in coil 2. From Faraday’s law of electromagnetic induction, this mutually induced emf ε₂ is given by

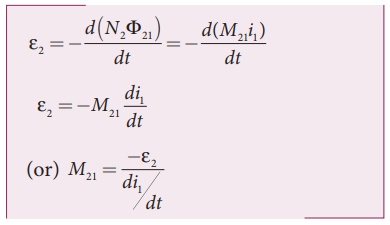
The negative sign in the above equation shows that the mutually induced emf always opposes the change in current i₁ with respect to time. If di₁/dt = 1 A s^-1, then M₂₁ = − ε .

Mutual inductance M₂₁ is also defined as the opposing emf induced in the coil 2 when the rate of change of current through the coil 1 is 1 As^-1.

Similarly, if an electric current i₂ through coil 2 changes with time, then emf ε₁ is induced in coil 1. Therefore,

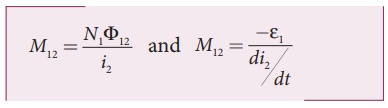
where M₁₂ is the mutual inductance of the coil 1 with respect to coil 2. It can be shown that for a given pair of coils, the mutual inductance is same.

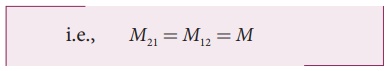
In general, the mutual induction between two coils depends on size, shape, the number of turns of the coils, their relative orientation and permeability of the medium.

Unit of mutual-inductance

The unit of mutual inductance is also henry (H).

If i₁ =1A and N ₂ Φ₂₁ =1 Wb turns, then M ₂₁ =1H .

Therefore, the mutual inductance between two coils is said to be one henry if a current of 1A in coil 1 produces unit flux linkage in coil 2.

If di₁/dt  = 1 As^−1  and ε₂ = −1 V , then M₂₁ = 1H.

Therefore, the mutual inductance between two coils is one henry if a current changing at the rate of 1 As^-1 in coil 1 induces an opposing emf of 1V in coil 2.