Analogies between LC oscillations and simple harmonic oscillations

Analogies between LC oscillations and simple harmonic oscillations

(i) Qualitative treatment

The electromagnetic oscillations of LC system can be compared with the mechanical oscillations of a spring-mass system.

There are two forms of energy involved in LC oscillations. One is electrical energy of the charged capacitor; the other magnetic energy of the inductor carrying current.

Likewise, the mechanical energy of the spring-mass system exists in two forms; the potential energy of the compressed or extended spring and the kinetic energy of the mass. The Table 4.3 lists these two pairs of energy.

By examining the Table 4.3, the analogies between the various quantities can be understood and these correspondences are given in the Table 4.4.

The angular frequency of oscillations of a spring-mass is given by (Refer equation 10.22 of section 10.4.1 of XI physics text book).

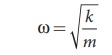
From Table 4.4, k → ¹/_C and m → L. Therefore, the angular frequency of LC oscillations is given by

(ii) Quantitative treatment

The mechanical energy of the spring-mass system is given by

The energy E remains constant for varying values of x and v. Differentiating E with respect to time, we get

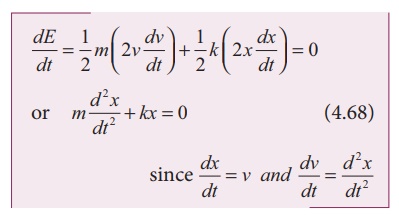
This is the differential equation of the oscillations of the spring-mass system. The general solution of equation (4.68) is of the form

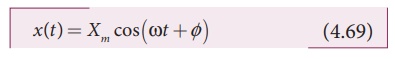
where X_m is the maximum value of x ( t ), the angular frequency and Ï• the phase constant.

Similarly, the electromagnetic energy of the LC system is given by

The general solution of equation (4.71) is of the form

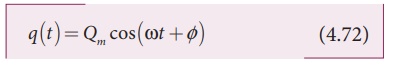
where Q_m  is the maximum value of q ( t ), the angular frequency and Ï• the phase constant.

Current in the LC circuit

The current flowing in the LC circuit is obtained by differentiating q(t) with respect to time.

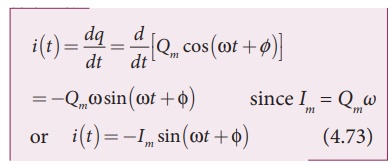
The equation (4.73) clearly shows that current varies as a function of time t. In fact, it is a sinusoidally varying alternating current with angular frequency ω.

Angular frequency of LC oscillations

By differentiating equation (4.72) twice, we get

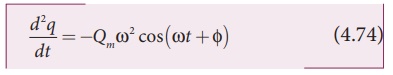
Substituting equations (4.72) and (4.74) in equation (4.71), we obtain

This equation is the same as that obtained from qualitative analogy.

Oscillations of electrical and magnetic energy

The electrical energy of the LC oscillator is

If the two energies are plotted with an assumption of f = 0 , we obtain Figure 4.58.

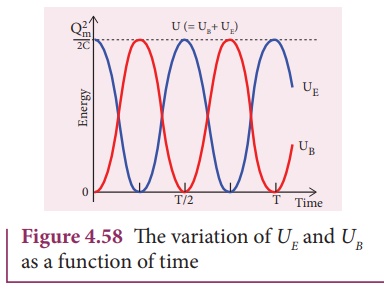
From the graph, it can be noted that

(i) At any instant U_E+U_B=Q_m²/2C = constant

(ii) The maximum values of U_E and U_B are both Q_m/2C

(iii) When U_E is Maximum, U_B is zero and vice versa.