RMS value of AC

RMS value of AC

The term RMS refers to time-varying sinusoidal currents and voltages and not used in DC systems.

The root mean square value of an alternating current is defined as the square root of the mean of the squares of all currents over one cycle. It is denoted by I_RMS . For alternating voltages, the RMS value is given by V_RMS.

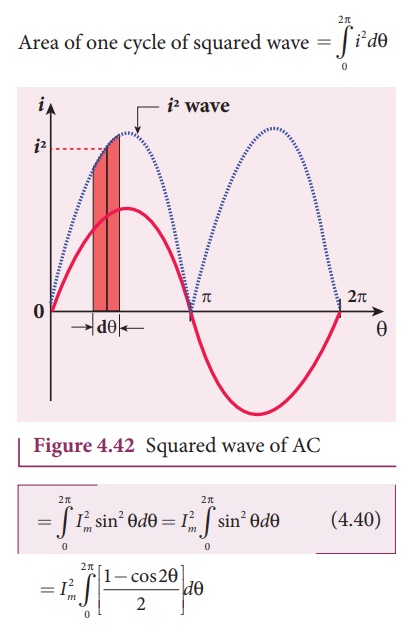
The alternating current i = I _m sin ω t or i = I_m sinθ ,  is represented graphically in Figure 4.42. The corresponding squared current wave is also shown by the dotted lines.

The sum of the squares of all currents over one cycle is given by the area of one cycle of squared wave. Therefore,

An elementary area of thickness dθ is considered in the first half-cycle of the squared current wave as shown in Figure 4.42. Let i² be the mid-ordinate of the element.

Area of the element = i 2dθ

Thus we find that for a symmetrical sinusoidal current rms value of current is 70.7 % of its peak value.

Similarly for alternating voltage, it can be shown that 

EXAMPLE 4.18

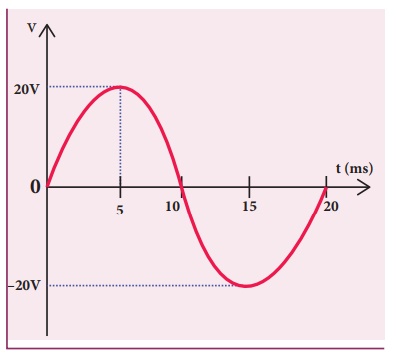
Write down the equation for a sinusoidal voltage of 50 Hz and its peak value is 20 V. Draw the corresponding voltage versus time graph.

Solution

EXAMPLE 4.19

The equation for an alternating current is given by i = 77 sin 314t. Find the peak value, frequency, time period and instantaneous value at t = 2 ms.

Solution

i = 77 sin 314t ; t = 2 ms = 2×10^-3 s

The general equation of an alternating current is i = I_m sin ωt . On comparsion,

(i) Peak value, I_m = 77 A

(ii) Frequency, f = ω/2π = 314 / 2 ×3.14 = 50 Hz

Time period, T = 1/f = 150 = 0 .02 s

(iv) At t = 2 m s,

Instantaneous value,

i = 77sin(314×2×10^−3 )

 i = 45.24 A

Phasor and phasor diagram

Phasor

A sinusoidal alternating voltage (or current) can be represented by a vector which rotates about the origin in anti-clockwise direction at a constant angular velocity ω. Such a rotating vector is called a phasor. A phasor is drawn in such a way that

·        the length of the line segment equals the peak value V_m (or I_m) of the alternating voltage (or current)

·        its angular velocity ω is equal to the angular frequency of the alternating voltage (or current)

·        the projection of phasor on any vertical axis gives the instantaneous value of the alternating voltage (or current)

·        the angle between the phasor and the axis of reference (positive x-axis) indicates the phase of the alternating voltage (or current).

The notion of phasors is introduced to analyse phase relationship between voltage and current in different AC circuits.

Phasor diagram

The diagram which shows various phasors and their phase relations is called phasor diagram. Consider a sinusoidal alternating voltage Ï… = V_m sin ωt applied to a circuit. This voltage can be represented by a phasor, namely  as shown in Figure 4.43.

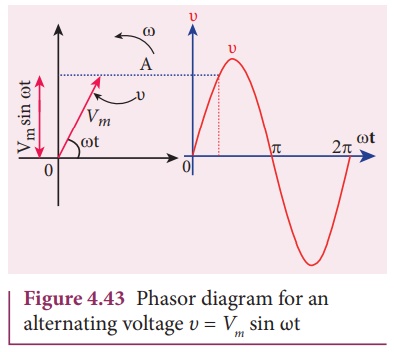
Here the length of  equals the peak value (V_m), the angle it makes with x-axis gives the phase (ωt) of the applied voltage. Its projection on y-axis provides the instantaneous value (V_m sin ωt) at that instant.

When  rotates about O with angular velocity ω in anti-clockwise direction, the waveform of the voltage is generated. For one full rotation of , one cycle of voltage is produced.

The alternating current in the same circuit may be given by the relation i = I_msin (ωt + Ï•) which is represented by another phasor . Here Ï• is the phase angle between voltage and current. In this case, the current leads the voltage by phase angle Ï• which is shown in Figure 4.44. If the current lags behind the voltage, then we write i = I_m sin (ωt - Ï•).