Coulomb’s Law

COULOMB’S LAW

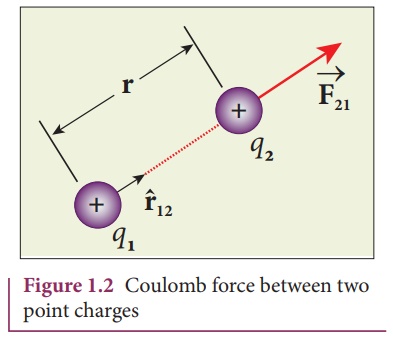
In the year 1786, Coulomb deduced the expression for the force between two stationary point charges in vacuum or free space. Consider two point charges q₁ and q₂ at rest in vacuum, and separated by a distance of r, as shown in Figure 1.2. According to Coulomb, the force on the point charge q₂ exerted by another point charge q₁ is

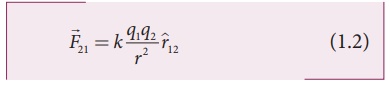
where ^r₁₂ is the unit vector directed from charge q₁ to charge q₂ and k is the proportionality constant.

Important aspects of Coulomb’s law

(i) Coulomb's law states that the electrostatic force is directly proportional to the product of the magnitude of the two point charges and is inversely proportional to the square of the distance between the two point charges.

(ii) The force on the charge q₂ exerted by the charge q₁ always lies along the line joining the two charges. ^r₁₂ is the unit vector pointing from charge q₁ to q₂. It is shown in the Figure 1.2. Likewise, the force on the charge q₁ exerted by q₂  is along -r^₁₂ (i.e., in the direction opposite to r^₁₂ ).

(iii) In SI units, 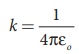 and its value is 9 × 10⁹ N m² C^-2. Here ε  is the permittivity of free space or vacuum and the value of 

(iv) The magnitude of the electrostatic force between two charges each of one coulomb and separated by a distance of 1 m is calculated as follows:

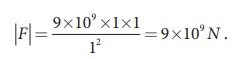
This is a huge quantity, almost equivalent to the weight of one million ton. We never come across 1 coulomb of charge in practice. Most of the electrical phenomena in day-to-day life involve electrical charges of the order of µC (micro coulomb) or nC (nano coulomb).

(v) In SI units, Coulomb’s law in vacuum takes the form 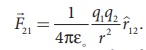 In a medium of permittivity ε, the force between two point charges is given by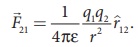 

Since ε>ε_o , the force  between two point charges in a medium other than vacuum is always less than that in vacuum. We define the relative permittivity for a given medium as ε_r>ε/ε_o . For vacuum or air, ε_r = 1 and ε for all other media ε_r> 1.

(vi) Coulomb’s law has same  structure as Newton’s law of gravitation. Both are inversely proportional to the square of the distance between the particles. The electrostatic force is directly proportional to the product of the magnitude of two point charges and gravitational force is directly proportional to the product of two masses. But there are some important differences between these two laws.

·        The gravitational force between two masses is always attractive but Coulomb force between two charges can be attractive or repulsive, depending on the nature of charges.

·        The value of the gravitational constant G = 6.626 × 10^-11 N m² kg^-2. The value of the constant k in Coulomb law is k = 9 × 10⁹ N m² C^-2. Since k is much more greater than G, the electrostatic force is always greater in magnitude than gravitational force for smaller size objects.

·        The gravitational force between two masses is independent of the medium. For example, if 1 kg of two masses are kept in air or inside water, the gravitational force between two masses remains the same. But the electrostatic force between the two charges depends on nature of the medium in which the two charges are kept at rest.

·        The gravitational force between two point masses is the same whether two masses are at rest or in motion. If the charges are in motion, yet another force (Lorentz force) comes into play in addition to coulomb force.

(vii) The force on a charge q₁ exerted by a point charge q₂ is given by

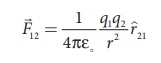
Here ^r₂₁ is the unit vector from charge q₂ to q₁.

But ^r₂₁ = − ^r₁₂ ,

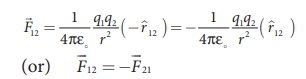
Therefore, the electrostatic force obeys Newton’s third law.

(viii) The expression for Coulomb force is true only for point charges. But the point charge is an ideal concept. However we can apply Coulomb’s law for two charged objects whose sizes are very much smaller than the distance between them. In fact, Coulomb discovered his law by considering the charged spheres in the torsion balance as point charges. The distance between the two charged spheres is much greater than the radii of the spheres.

EXAMPLE 1.2

Consider two point charges q1 and q2 at rest as shown in the figure.

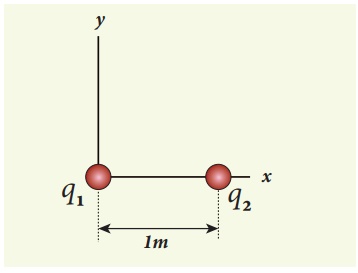
They are separated by a distance of 1m. Calculate the force experienced by the two charges for the following cases:

(a) q₁ = +2μC and q₂ = +3μC

(b) q₁ = +2μC and q₂ = -3μC

(c) q₁= +2μC and q₂ = -3μC kept in water (ε_r = 80)

Solution

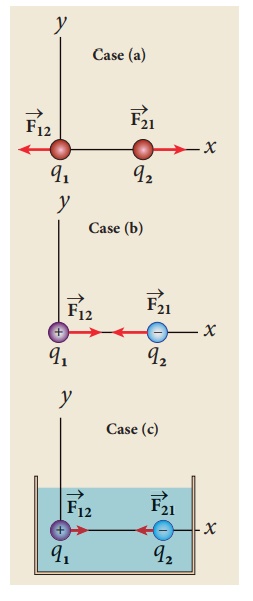
EXAMPLE 1.3

Two small-sized identical equally charged spheres, each having mass 1 mg are hanging in equilibrium as shown in the figure. The length of each string is 10 cm and the angle θ is 7° with the vertical. Calculate the magnitude of the charge in each sphere.

(Take g = 10 ms^−2)

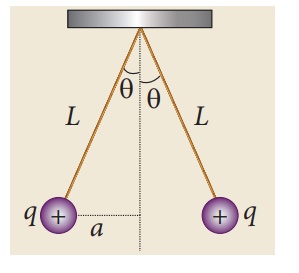
Solution

If the two spheres are neutral, the angle between them will be 0o when hanged vertically. Since they are positively charged spheres, there will be a repulsive force between them and they will be at equilibrium with each other at an angle of 7° with the vertical. At equilibrium, each charge experiences zero net force in each direction. We can draw a free body diagram for one of the charged spheres and apply Newton’s second law for both vertical and horizontal directions.

The free body diagram is shown below.

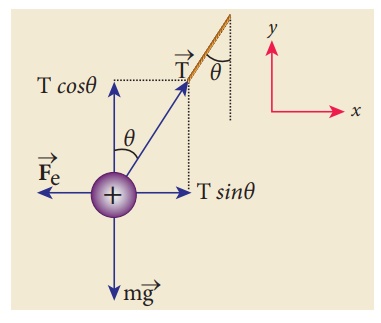
In the x-direction, the acceleration of the charged sphere is zero. 

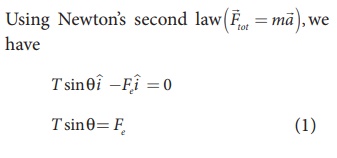
Here T is the tension acting on the charge due to the string and F_e is the electrostatic force between the two charges.

In the y-direction also, the net acceleration experienced by the charge is zero.

EXAMPLE 1.4

Calculate the electrostatic force and gravitational force between the proton and the electron in a hydrogen atom. They are separated by a distance of 5.3 × 10^-11 m. The magnitude of charges on the electron and proton are 1.6 × 10^-19 C. Mass of the electron is m_e = 9.1 × 10^-31 kg and mass of proton is m_p = 1.6 × 10^-27 kg.

Solution

The proton and the electron attract each other. The magnitude of the electrostatic force between these two particles is given by

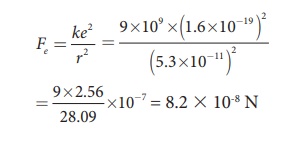
The gravitational force between the proton and the electron is attractive. The magnitude of the gravitational force between these particles is

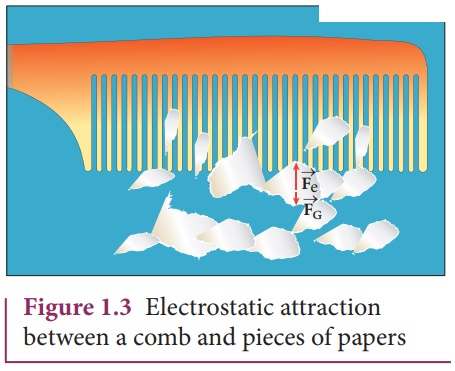
The electrostatic force between a proton and an electron is enormously greater than the gravitational force between them. Thus the gravitational force is negligible when compared with the electrostatic force in many situations such as for small size objects and in the atomic domain. This is the reason why a charged comb attracts an uncharged piece of paper with greater force even though the piece of paper is attracted downward by the Earth. This is shown in Figure 1.3

1. Superposition principle

Coulomb’s law explains the interaction between two point charges. If there are more than two charges, the force on one charge due to all the other charges needs to be calculated. Coulomb’s law alone does not give the answer. The superposition principle explains the interaction between multiple charges.

According to this superposition principle, the total force acting on a given charge is equal to the vector sum of forces exerted on it by all the other charges.

Consider a system of n charges, namely q₁, q₂, q₃ ….q_n. The force on q₁ exerted by the charge q₂

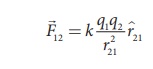
Here ^r₂₁ is the unit vector from q₂ to q₁ along the line joining the two charges and r₂₁ is the distance between the charges q₁ and q₂. The electrostatic force between two charges is not affected by the presence of other charges in the neighbourhood.

The force on q₁ exerted by the charge q₃ is

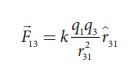
By continuing this, the total force acting on the charge q₁ due to all other charges is given by

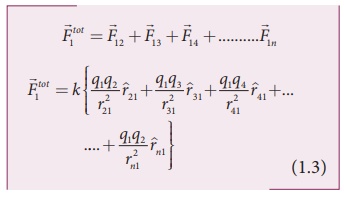
EXAMPLE 1.5

Consider four equal charges q₁,q₂, q₃ and q₄ = q = +1μC located at four different points on a circle of radius 1m, as shown in the figure. Calculate the total force acting on the charge q₁ due to all the other charges.

Solution

According to the superposition principle, the total electrostatic force on charge q1 is the vector sum of the forces due to the other charges,

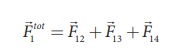
The following diagram shows the direction of each force on the charge q₁.

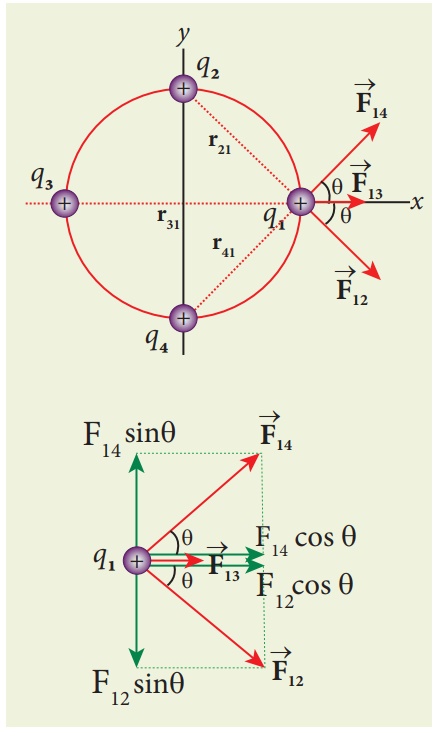
The charges q₂ and q₄ are equi-distant from q₁. As a result the strengths (magnitude) of the forces  and  are the same even though their directions are different. Therefore the vectors representing these two forces are drawn with equal lengths. But the charge q₃ is located farther compared to q₂ and q₄. Since the strength of the electrostatic force decreases as distance increases, the strength of the force  is lesser than that of forces  and  . Hence the vector representing the force  is drawn with smaller length compared to that for forces  and .

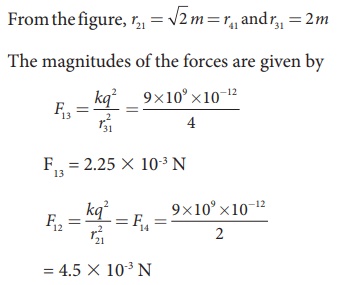
From the figure, the angle θ = 45º. In terms of the components, we have

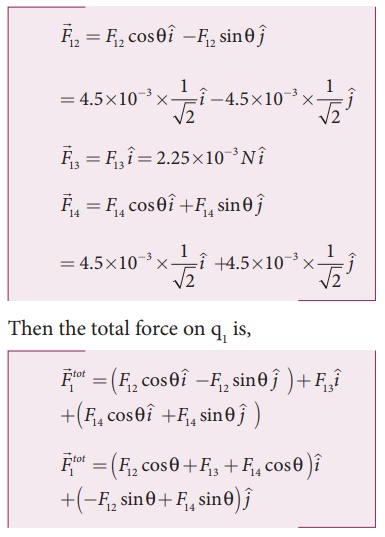
Since F₁₂ = F₁₄, the j^th component is zero.

Hence we have

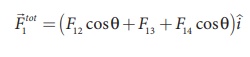
substituting the values in the above equation,

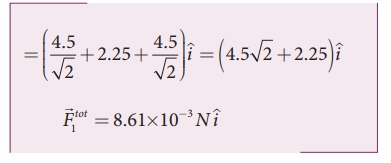
The resultant force is along the positive x axis.