Chapter: 11th Physics : UNIT 8 : Heat and Thermodynamics
Boyle’s law, Charles’ law and ideal gas law - Thermal Properties of Matter
THERMAL
PROPERTIES OF MATTER
Boyle’s
law, Charles’ law and ideal gas law
For
a given gas at low pressure (density) kept in a container of volume V,
experiments revealed the following information.
·
When
the gas is kept at constant temperature, the pressure of the gas is inversely proportional
to the volume. P ‚àù 1/V. It was discovered by Robert Boyle
(1627-1691) and is known as Boyle’s law.
·
When
the gas is kept at constant pressure, the volume of the gas is directly
proportional to absolute temperature. V ‚àùT .
It was discovered by Jacques Charles (1743-1823) and is known as
Charles’ law.
·
By
combining these two equations we have
PV =
CT. Here C is a positive constant.
We
can infer that C is proportional to the number of particles in the gas
container by considering the following argument. If we take two containers of
same type of gas with same volume V, same pressure P and same temperature T,
then the gas in each container obeys the above equation. PV = CT. If the two
containers of gas is considered as a
single system, then the pressure and temperature of this combined system will
be same but volume will be twice and number of particles will also be double as
shown in Figure 8.2
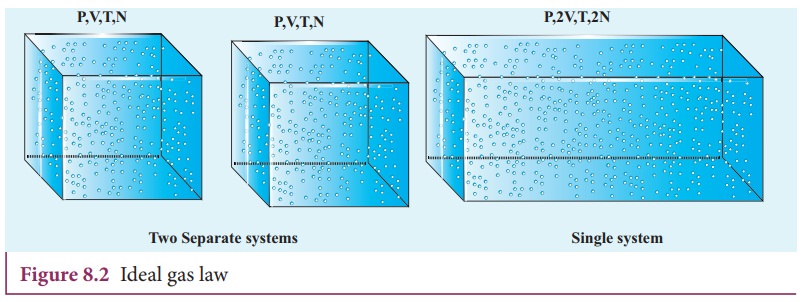
For
this combined system, V becomes 2V, so C should also double to match with the
ideal gas equation P(2V) / T = 2C . It implies that C must depend on the number of particles in the
gas and also should have the dimension of [PV/T] = JK-1. So we can
write the constant C as k times the number of particles N.
Here
k is the Boltzmann constant (1.381√ó10‚àí23 JK‚àí1) and it is
found to be a universal constant.
So
the ideal gas law can be stated as follows

The
equation (8.1) can also be expressed in terms of mole.
Suppose
if a gas contains μ mole of particles then the total number of particles can be
written as

where
NA is Avogadro number
(6.023 √ó1023mol-1)
Substituting
for N from equation (8.2), the equation (8.1) becomes
PV = μ NAkT. Here NAk=R called universal gas
constant and its value is 8.314 J /mol. K.
So
the ideal gas law can be written for μ mole of gas as

This
is called the equation of state for an ideal gas. It relates the pressure,
volume and temperature of thermodynamic system at equilibrium.
EXAMPLE 8.2
A
student comes to school by a bicycle whose tire is filled with air at a
pressure 240 kPa at 27°C. She travels 8 km to reach the school and the
temperature of the bicycle tire increases to 39°C. What is the change in
pressure in the tire when the student reaches school?

Solution
We
can take air molecules in the tire as an ideal gas. The number of molecules and
the volume of tire remain constant. So the air molecules at 27°C satisfies the
ideal gas equation P1V1 = NkT1 and at 39°C it satisfies P2V2
= NkT2
But
we know
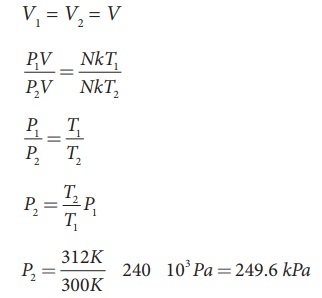
EXAMPLE 8.3
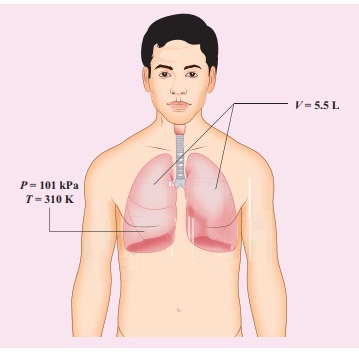
When
a person breaths, his lungs can hold up to 5.5 Litre of air at body temperature
37°C and atmospheric pressure (1 atm =101 kPa). This Air contains 21% oxygen.
Calculate the number of oxygen molecules in the lungs.
Solution
We
can treat the air inside the lungs as an ideal gas. To find the number of
molecules, we can use the ideal gas law.
PV =
NkT
Here
volume is given in the Litre. 1 Litre is volume occupied by a cube of side 10
cm. 1Litre = 10cm √ó 10cm √ó 10cm = 10-3 m3
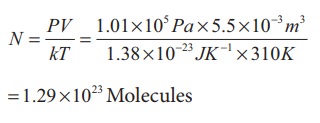
Only
21% of N are oxygen. The total number of oxygen molecules
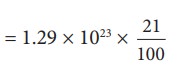
Number
of oxygen molecules = 2.7 √ó 1022 molecules
EXAMPLE 8.4
Calculate
the volume of one mole of any gas at STP and at room temperature (300K) with the
same pressure 1 atm.
Solution:
Here
STP means standard temperature (T=273K or 0°C) and Pressure (P=1 atm or 101.3
kPa)
We
can use ideal gas equation V = μRT / P.
By
substituting the values
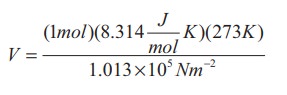
=22.4
√ó 10-3 m3
We
know that 1 Litre (L) = =10-3m3. So we can conclude that
1 mole of any ideal gas has volume 22.4 L.
By
multiplying 22.4L by 300/273KK we get the volume of one mole of gas at room
temperature. It is 24.6 L.
EXAMPLE 8.5
Estimate
the mass of air in your class room at NTP. Here NTP implies normal temperature
(room temperature) and 1 atmospheric pressure.

Solution
The average size of a class is 6m length, 5 m breadth and 4 m height. The volume of the room V = 6 √ó 5 √ó 4 = 120m3. We can determine the number of mole. At room temperature 300K, the volume of a gas occupied by any gas is equal to 24.6L.
The
number of mole μ=
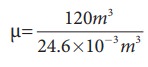
≈4878
mol .
Air
is the mixture of about 20% oxygen, 79% nitrogen and remaining one percent are
argon, hydrogen, helium, and xenon. The molar mass of air is 29 gmol-1.
So
the total mass of air in the room m =
4878 √ó 29 = 141.4kg.
Related Topics