Definition, Explanation, Formulas, Solved Example Problems | Alternating Current (AC) - Quality factor or QŌĆōfactor | 12th Physics : Electromagnetic Induction and Alternating Current
Chapter: 12th Physics : Electromagnetic Induction and Alternating Current
Quality factor or QŌĆōfactor
Quality factor or QŌĆōfactor
The current in the
series RLC circuit becomes maximum at resonance. Due to the increase in
current, the voltage across L and C are also increased. This
magnification of voltages at series resonance is termed as QŌĆōfactor.
It is defined as the
ratio of voltage across L or C to the applied voltage.
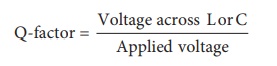
Q-factor = Voltage across LorC /
Applied voltage
At resonance, the
circuit is purely resistive. Therefore, the applied voltage is equal to the
voltage across R.
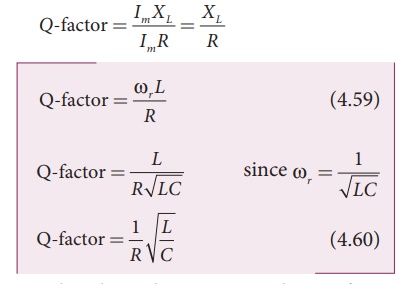
The physical meaning is
that QŌĆōfactor indicates the number of times the voltage across L or C
is greater than the applied voltage at resonance.
Since the phase angle is positive,
voltage leads current by 53.1 for this inductive circuit.
EXAMPLE 4.22
Find the impedance of a
series RLC circuit if the inductive reactance, capacitive reactance and
resistance are 184 ╬®, 144 ╬® and 30 ╬® respectively. Also calculate the phase
angle between voltage and current.
Solution
XL = 184 ╬®; XC
= 144 ╬®
R = 30 ╬®
(i ) The impedance is
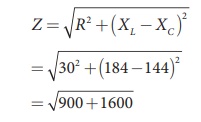
Impedance, Z = 50 Ōä”
(ii) Phase angle is
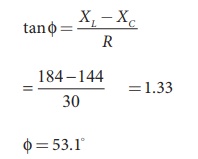
Žå = 53.1
EXAMPLE 4.23
A 500 ╬╝H inductor, 80/ŽĆ2
pF capacitor and a 628 ╬® resistor are connected to form a series RLC circuit.
Calculate the resonant frequency and Q-factor of this circuit at resonance.
Solution
L=500├Ś10-6H;
C = 80/ŽĆ2 ├Ś10ŌłÆ12 F; R = 628Ōä”
(i) Resonant frequency
is

Q =12.5
EXAMPLE 4.24
Find the instantaneous
value of alternating voltage Žģ = 10 sin(3 ŽĆ├Ś104 t) volt at i) 0ŌĆås
ii) 50 ╬╝s iii) 75 ╬╝s.
Solution
The given equation is Žģ
= 10sin (3 ŽĆ├Ś104 t)

EXAMPLE 4.25
The current in an
inductive circuit is given by 0.3 sin (200t ŌĆō 40┬░) A. Write the equation for
the voltage across it if the inductance is 40 mH.
Solution
L = 40 ├Ś 10-3
H; i = 0.1 sin (200t ŌĆō 40┬║)
XL = ŽēL = 200
├Ś 40 ├Ś 10-3 = 8 Ōä”
Vm = Im
XL = 0.3 ├Ś 8 = 2.4 V
In an inductive circuit,
the voltage leads the current by 90o Therefore,
v = Vm sin ( Žēt +90┬║)
v =
2 . 4 sin(200t ŌłÆ40 + 90 ┬║)
v = 2 . 4 sin(200t +50 ┬║)volt
Related Topics