Definition, Explanation, Solved Example Problems | Electromagnetic Induction - Motional emf from FaradayŌĆÖs law and Energy conservation | 12th Physics : Electromagnetic Induction and Alternating Current
Chapter: 12th Physics : Electromagnetic Induction and Alternating Current
Motional emf from FaradayŌĆÖs law and Energy conservation
Motional emf from FaradayŌĆÖs law and Energy
conservation
Let us consider a
rectangular conducting loop of width l in a uniform magnetic field ![]() which is perpendicular to the plane of the loop and is directed inwards. A part
of the loop is in the magnetic field while the remaining part is outside the
field as shown in Figure 4.10.
which is perpendicular to the plane of the loop and is directed inwards. A part
of the loop is in the magnetic field while the remaining part is outside the
field as shown in Figure 4.10.
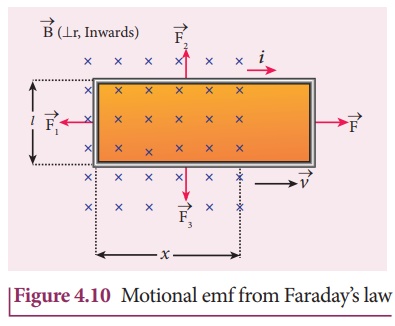
When the loop is pulled
with a constant velocity ![]() to the right, the area of the
portion of the loop within the magnetic field will decrease. Thus, the flux
linked with the loop will also decrease. According to FaradayŌĆÖs law, an
electric current is induced in the loop which flows in a direction so as to
oppose the pull of the loop.
to the right, the area of the
portion of the loop within the magnetic field will decrease. Thus, the flux
linked with the loop will also decrease. According to FaradayŌĆÖs law, an
electric current is induced in the loop which flows in a direction so as to
oppose the pull of the loop.
Let x be the
length of the loop which is still within the magnetic field, then its area is lx
. The magnetic flux linked with the loop is
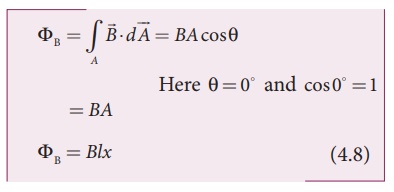
As this magnetic flux
decreases due to the movement of the loop, the magnitude of the induced emf is
given by
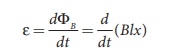
Here, both B and
l are constants. Therefore,

where v = dx/dt is the
velocity of the loop.![]()
![]()
This emf is known as
motional emf since it is produced due to the movement of the loop in the
magnetic field.
From LenzŌĆÖs law, it is
found that the induced current flows in clockwise direction. If R is the
resistance of the loop, then the induced current is given by

Energy conservation
In order to move the
loop with a constant velocity ![]() , a constant force
that is equal and opposite to the magnetic force, must be applied. Therefore,
mechanical work is done to move the loop. Then the rate of doing work or power
is
, a constant force
that is equal and opposite to the magnetic force, must be applied. Therefore,
mechanical work is done to move the loop. Then the rate of doing work or power
is

Now, let us find the
magnetic force acting on the loop due to its movement in the magnetic field.
Let three deflecting forces ![]() 1 ,
1 , ![]() 2
and
2
and ![]() 3 be acting on the three segments of
the loop as shown in Figure 4.10. The general equation of such a deflecting
force is given by
3 be acting on the three segments of
the loop as shown in Figure 4.10. The general equation of such a deflecting
force is given by
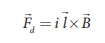
Forces ![]() 2 and
2 and ![]() 3 are equal in magnitude and opposite in
direction and cancel each other. Therefore, the force
3 are equal in magnitude and opposite in
direction and cancel each other. Therefore, the force ![]() 1
alone acts on the left segment of the loop in a direction shown in Figure 4.10
and is given by
1
alone acts on the left segment of the loop in a direction shown in Figure 4.10
and is given by

Here ╬Ė is the angle between ![]() and the length vector
and the length vector ![]() for the left
segment and is 90┬║
for the left
segment and is 90┬║
Ōł┤ F1 = il Bsin90┬║ =il B since sin90┬║ = 1
The applied force ![]() must be equal to
must be equal to ![]() in order to just move the
loop with a 1 constant velocity
in order to just move the
loop with a 1 constant velocity ![]()
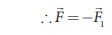
(since ![]() and
and ![]() 1
are in opposite direction)
1
are in opposite direction)
Considering only the
magnitudes,
F = F1 = i l B
Substituting for i from
equation (4.10)
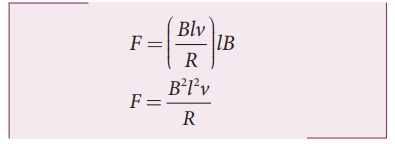
From equation (4.11),
the rate at which the mechanical work is done to pull the loop from the
magnetic field or power is given by
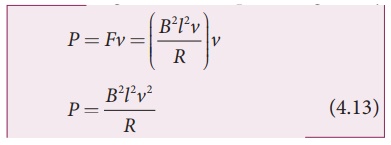
When the induced current
flows in the loop, Joule heating takes place. The rate at which thermal energy
is dissipated in the loop or power dissipated is
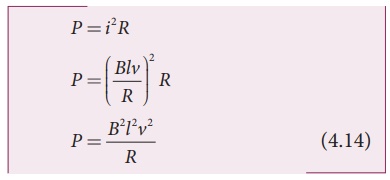
This equation is exactly
same as the equation (4.13). Thus the mechanical work done in moving
the loop appears as thermal energy in the loop.
EXAMPLE 4.8
A conducting rod of
length 0.5 m falls freely from the top of a building of height 7.2 m at a place
in Chennai where the horizontal component of EarthŌĆÖs magnetic field is 40378.7
nT. If the length of the rod is perpendicular to EarthŌĆÖs horizontal magnetic
field, find the emf induced across the conductor when the rod is about to touch
the ground. [Take g = 10 m s-2]
Solution
l = 0.5 m; h = 7.2 m; u =
0 m s-1;
g = 10 m s-2;
BH = 40378.7 nT
The final velocity of
the rod is
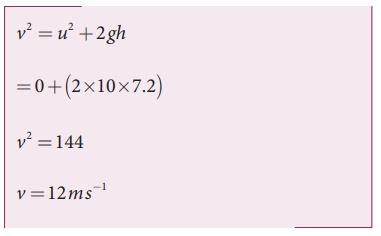
Induced emf when the rod
is about to touch the ground, ╬Ą = BH lv
= 40, 378.7 ├Ś10ŌłÆ9
├Ś 0.5 ├Ś12
=242 .27 ├Ś10ŌłÆ6V
=242 .27┬ĄV
EXAMPLE 4.9
A copper rod of length l
rotates about one of its ends with an angular velocity Žē in a magnetic field B
as shown in the figure. The plane of rotation is perpendicular to the field.
Find the emf induced between the two ends of the rod.
Solution
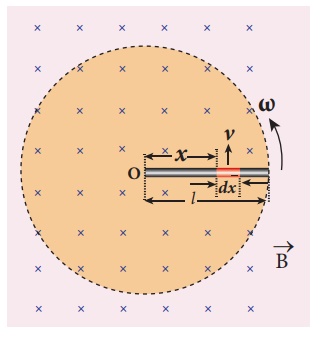
Consider a small element
of length dx at a distance x from the centre of the circle
described by the rod. As this element moves perpendicular to the field with a
linear velocity v = xŽē , the emf
developed in the element dx is
d ╬Ą = Bvdx = B( xŽē)dx
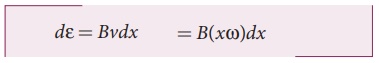
This rod is made up of
many such elements, moving perpendicular to the field. The emf developed across
two ends is
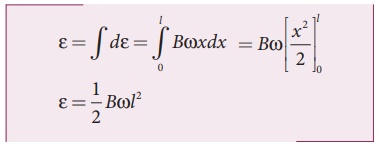
Related Topics