Waves: Important Questions

Short Answer Questions

1. What is meant by waves?.

2. Write down the types of waves.

3. What are transverse waves?. Give one example.

4. What are longitudinal waves?. Give one example.

5. Define wavelength.

6. Write down the relation between frequency, wavelength and velocity of a wave.

7. What is meant by interference of waves?.

8. Explain the beat phenomenon.

9. Define intensity of sound and loudness of sound.

10. Explain Doppler Effect.

11. Explain red shift and blue shift in Doppler Effect.

12. What is meant by end correction in resonance air column apparatus?

13. Sketch the function y = x + a. Explain your sketch.

14. Write down the factors affecting velocity of sound in gases.

15. What is meant by an echo?. Explain.

Long Answer Questions

1. Discuss how ripples are formed in still water.

2. Briefly explain the difference between travelling waves and standing waves.

3. Show that the velocity of a travelling wave produced in a string is v = √[T/μ]

4. Describe Newton’s formula for velocity of sound waves in air and also discuss the Laplace’s correction.

5. Write short notes on reflection of sound waves from plane and curved surfaces.

6. Briefly explain the concept of superposition principle.

7. Explain how the interference of waves is formed.

8. Describe the formation of beats.

9. What are stationary waves?. Explain the formation of stationary waves and also write down the characteristics of stationary waves.

10. Discuss the law of transverse vibrations in stretched strings.

11. Explain the concepts of fundamental frequency, harmonics and overtones in detail.

12. What is a sonometer?. Give its construction and working. Explain how to determine the frequency of tuning fork using sonometer.

13. Write short notes on intensity and loudness.

14. Explain how overtones are produced in a

(a) Closed organ pipe

(b) Open organ pipe

15. How will you determine the velocity of sound using resonance air column apparatus?

16. What is meant by Doppler effect?.

Discuss the following cases

(1) Source in motion and Observer at rest

(a) Source moves towards observer

(b) Source moves away from the observer

(2) Observer in motion and Source at rest.

(a) Observer moves towards Source

(b) Observer resides away from the Source

(3) Both are in motion

(a) Source and Observer approach each other

(b) Source and Observer resides from each other

(c) Source chases Observer

(d) Observer chases Source

Numerical Problems

 

1. The speed of a wave in a certain medium is 900 m/s. If 3000 waves passes over a certain point of the medium in 2 minutes, then compute its wavelength?.

Solution

The speed of a wave in medium v = 900 ms-1

Freq. of wave = no. of waves passing per sec (n) = 3000 waves/2min = 3000 / 2×60 = 25s

Wave length = λ =?

v = n λ

λ  = v/n

A = 900/25 =36m

A = 36m

Answer : λ = 36 m

 

2. Consider a mixture of 2 mol of helium and 4 mol of oxygen. Compute the speed of sound in this gas mixture at 300 K.

Solution

Helium - 2 mole, oxygen - 4 mol

He & O2 are mixed, hence molecular weight of the mixture of gases

Answer : 400.9 ms-1

 

3. A ship in a sea sends SONAR waves straight down into the seawater from the bottom of the ship. The signal reflects from the deep bottom bed rock and returns to the ship after 3.5 s. After the ship moves to 100 km it sends another signal which returns back after 2s. Calculate the depth of the sea in each case and also compute the difference in height between two cases.

Solution

Velocity of SONAR waves in water C = 1500 ms-1

Time taken by be wave after reflection from the bottom of sea

2t = 3.5s

t =1.75s

Distance covered (d) = ?

C = d/t => d = c.t = 1500 × 1.75 - 2625 m

After moving 100km

The time taken by the wave = 2t = 2s

T  = 2/2 = 1s

d =?

d = 1500 × l

= 1500

The different between these two heights . = 2625 - 1500

= 1125m

Answer : Δd = 1149.75 m

 

4. A sound wave is transmitted into a tube as shown in figure. The sound wave splits into two waves at the point A which recombine at point B. Let R be the radius of the semi-circle which is varied until the first minimum. Calculate the radius of the semi-circle if the wavelength of the sound is 50.0 m.

Answer : R = 21.9 m

Solution

Consider the sound waves start from the pt A. The sound waves will meet at the picture B & interfere and can be detected.

The path length of sound waves passing through the curve is equal to half the circle having radio centered at c.

Thus, be path length of be sound waves in curve part is

L1 = πγ

The path length of the sound in tube ABC is equal to the diameter of the circle having radius γ centered at e.

So the path length of the sound waves travelling in it = L2 =2r

The path difference of the sound waves at the picture is

ΔP = L1 - L2

= πr— 2r

ΔP = r(π - 2) ...(1)

For the sound to be heard minimum at the detected the difference in path length of be sound waves is

ΔP = λ/2    …………(2)

From equation (1)

r(π- 2) = λ/2

wavelength of sound = λ = 50m

radius of be semicircle r = ?

r = 50 / [2 × 3.14 – 4] = 50/2.28

r = 21.9m

Answer : R = 21.9 m

 

5.   N tuning forks are arranged in order of increasing frequency and any two successive tuning forks give n beats per second when sounded together. If the last fork gives double the frequency of the first (called as octave), Show that the frequency of the first tuning fork is f = (N−1)n.

Solution

No.of tuning forks = N

The frequency of the first is double to be last

The difference of frequency for two successive tuning forks NHz

Let be frequency of the first tuning fork is f

Then be frequency of the last tuning fork is f(N-l)n

frequency is reduced to are fourth

flast = - f /2 

an = a + (n-1)d

(i.e.) 2f  =  f + (N-1)n

= (N-1)n

f = (N-1)n

 

6.   Let the source propagate a sound wave whose intensity at a point (initially) be I. Suppose we consider a case when the amplitude of the sound wave is doubled and the frequency is reduced to one-fourth. Calculate now the new intensity of sound at the same point ?.

Solution

Intensity of sound wave  = Iold

Amplitude is doubled = 2A = Anew

Frequency is produced to are fourth

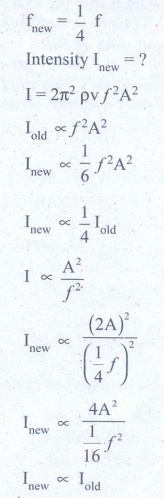
Answer: Inew ∝ ¼ I old

 

7. Consider two organ pipes of same length in which one organ pipe is closed and another organ pipe is open. If the fundamental frequency of closed pipe is 250 Hz. Calculate the fundamental frequency of the open pipe.

Answer: 500Hz

 

8. A police in a siren car moving with a velocity 20 ms-1 chases a thief who is moving in a car with a velocity v0ms-1. The police car sounds atfrequency 300Hz, and both of them move towards a stationary siren of frequency 400Hz. Calculate the speed in which thief is moving.

Solution

The velocity of car = 20ms-1

The frequency of car = 300Hz

The frequency stationary siren = 400Hz

The speed in which thief moving = ?

Answer: vthief = 10 m s-1

 

9. Consider the following function

(a) y = x2 + 2 α t x

(b) y = (x + vt)2

which among the above function can be characterized as a wave ?.

Solution

(a) y = x2 + 2 a t x

It is not describing wave.

(b) y = (x + 2 vx)2

It satisfies wave equation.

Answer: (a) function is not describing wave (b) satisfies wave equation.

 

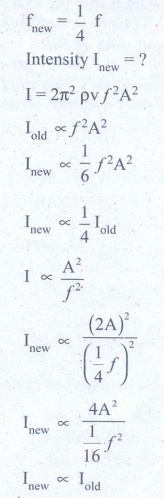
Conceptual Questions

 

1. Why is it that transverse waves cannot be produced in a gas?. Can the transverse waves can be produced in solids and liquids?

Answer: Transverse waves travel in the form of crests and troughs and so involve change in shape. As gas has no elasticity of shape, transverse waves cannot be produced in it.

2. Why is the roar of our national animal different from the sound of a mosquito?

Answer: Roaring of a national animal (tiger) produces a sound of low pitch and high intensity or loudness, whereas the buzzing of mosquito produces a sound of high pitch and low intensity or loudness.

3. A sound source and listener are both stationary and a strong wind is blowing. Is there a Doppler effect?

Answer: Yes. It does not matter whether there is sound I source or transmission media in motion.

4. In an empty room why is it that a tone sounds louder than in the room having things like furniture etc.

Answer: Sound is a form of energy. The furniture which act as obstacles absorbs most of the energy. So the intensity of sound become low but in empty room, due to the absence of obstacles the intensity of sound remain mostly same and we feel it louder.

5. How do animals sense impending danger of hurricane? 

Answer: Some animals are believed to be sensitive to low frequency sound waves emitted by hurricanes. They can also detect the slight fall in air pressure, and water pressure that signal a storm's approach.

6. Is it possible to realize whether a vessel kept under the tap is about to fill with water?

Answer: The frequency of the note produced by an air column is inversely proportional to its length. As the level of water in the vessel rises, the length of the air column above it decreases. It produce, sound of decreasing frequency, i.e., the sound becomes shorter. From the shrillness of sound, is possible to realize whether the vessel is filled with water.

vmin = 11.71 ms-1