Chapter: 11th Physics : UNIT 11 : Waves
Velocity of Waves in Different Media
Suppose
a hammer is stroked on long rails at a distance and when a person keeps his ear
near the rails at the other end he/she will hear two sounds, at different
instants. The sound that is heard through the rails (solid medium) is faster
than the sound we hear through the air (gaseous medium). This implies the
velocity of sound is different in different media.
In
this section, we shall derive the velocity of waves in two different cases:
1.
The velocity of a transverse waves along a stretched string.
2.
The velocity of a longitudinal waves in an elastic medium.
1. Velocity of transverse waves in a stretched string
Let
us compute the velocity of transverse travelling waves on a string. When a jerk
is given at one end (left end) of the rope, the wave pulses move towards right
end with a velocity v as shown in the
Figure 11.15 (a). This means that the pulses move with a velocity v with respect to an observer who is at
rest frame. Suppose an observer also moves with same velocity v in the direction of motion of the wave
pulse, then that observer will notice that the wave pulse is stationary and the
rope is moving with pulse with the same velocity v.
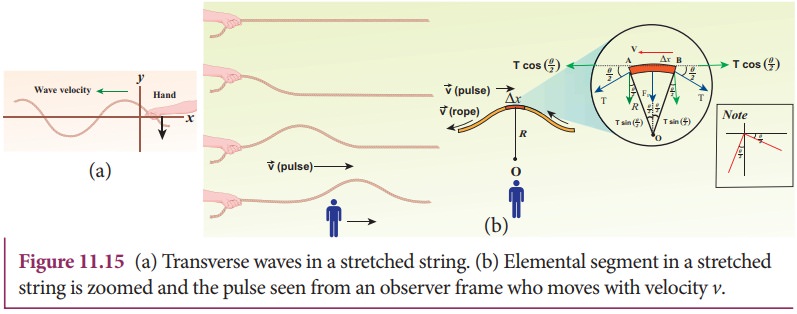
Consider
an elemental segment in the string as shown in the Figure 11.15 (b). Let A and
B be two points on the string at an instant of time. Let dl and dm be the length
and mass of the elemental string, respectively. By definition, linear mass
density, μ is

The
elemental string AB has a curvature which looks like an arc of a circle with
centre at O, radius R and the arc subtending an angle θ at the origin O as
shown in Figure 11.15(b). The angle θ can be written in terms of arc length and
radius as θ = dl/R. The centripetal
acceleration supplied by the tension in the string is

Then,
centripetal force can be obtained when mass of the string (dm) is included in
equation (11.7)

The
centripetal force experienced by elemental string can be calculated by
substituting equation (11.6) in equation (11.8) we get

The
tension T acts along the tangent of the elemental segment of the string at A
and B. Since the arc length is very small, variation in the tension force can
be ignored. We can resolve T into horizontal component Tcos(θ/2) and vertical
component T sin(θ/2).
The
horizontal components at A and B are equal in magnitude but opposite in
direction; therefore, they cancel each other. Since the elemental arc length AB
is taken to be very small, the vertical components at A and B appears to acts
vertical towards the centre of the arc and hence, they add up. The net radial
force Fr is
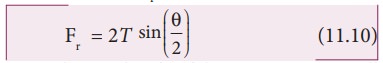
Since
the amplitude of the wave is very small when it is compared with the length of
the string, the sine of small angle is approximated as sin(θ/2)≈ θ/2. Hence,
equation (11.10) can be written as
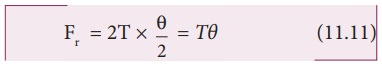
But
θ = dl/R, therefore substituting in
equation (11.11), we get

Applying
Newton’s second law to the elemental
string in the radial direction, under equilibrium, the radial component of the
force is equal to the centripetal force. Hence equating equation (11.9) and
equation (11.12), we have

Observations:
The
velocity of the string is
a.
directly proportional to the square root of the tension force
b.
inversely proportional to the square root of linear mass density
c.
independent of shape of the waves.
EXAMPLE 11.6
Calculate
the velocity of the travelling pulse as shown in the figure below. The linear
mass density of pulse is 0.25 kg m-1. Further, compute the time
taken by the travelling pulse to cover a distance of 30 cm on the string.

Solution
The
tension in the string is T = m g = 1.2 × 9.8 = 11.76 N
The
mass per unit length is μ = 0.25 kg m-1.
Therefore, velocity of the wave pulse is
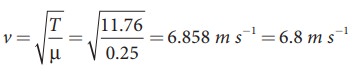
The
time taken by the pulse to cover the distance of 30 cm is
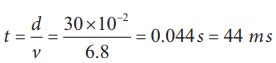
where
ms
= milli second.
2. Velocity of longitudinal waves in an elastic medium
Consider
an elastic medium (here we assume air) having a fixed mass contained in a long
tube (cylinder) whose cross sectional area is A and maintained under a pressure P. One can generate
longitudinal waves in the fluid either by displacing the fluid using a piston
or by keeping a vibrating tuning fork at one end of the tube. Let us assume
that the direction of propagation of waves coincides with the
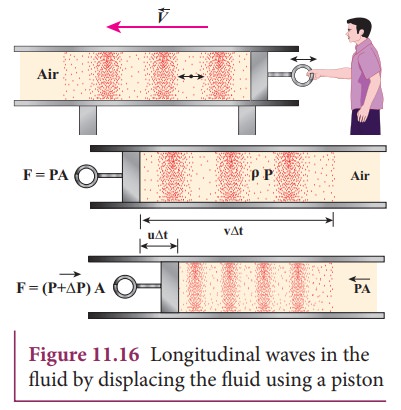
Let ρ be the density
of the fluid which is initially at rest. At t
= 0, the piston at left end of the tube is set in motion toward the right with
a speed u.
Let
u be the velocity of the piston and v be the velocity of the elastic wave.
In time interval ∆t, the distance moved by the piston ∆d = u∆t. Now, the distance moved by the elastic disturbance is ∆x = v∆t. Let m be
the mass of the air that has attained a velocity v in a time ∆t . Therefore,
m = ρ A∆x
= ρ A (v∆t)
Then,
the momentum imparted due to motion of piston with velocity u is
p = [ρ
A (v t)]u
But
the change in momentum is impulse.
The
net impulse is
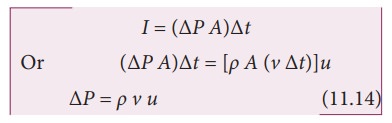
When
the sound wave passes through air, the small volume element (ΔV) of the air undergoes regular
compressions and rarefactions. So, the change in pressure can also be written
as
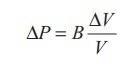
where,
V is original volume and B is known as bulk modulus of the elastic medium.
But
V = A ∆x = A v ∆t
and
∆V = A
∆d =A u ∆t
Therefore,

Comparing
equation (11.14) and equation (11.15), we get
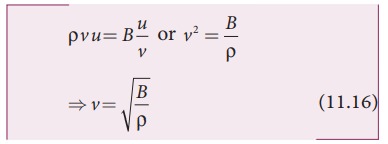
In
general, the velocity of a longitudinal wave in elastic medium is v = √E/√P where
E is the modulus of elasticity of the
medium.
Cases: For a solid :
(i) one dimension rod (1D)

where
Y is the Young’s modulus of the
material of the rod and ρ is the
density of the rod. The 1D rod will have only Young’s modulus.
(ii)Three dimension rod (3D) The speed of longitudinal wave in a solid is
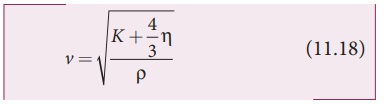
where
η is the modulus of rigidity, K is
the bulk modulus and ρ is the density
of the rod.
Cases: For liquids:
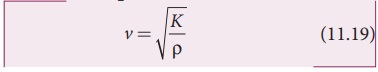
where,
K is the bulk modulus and ρ is the density of the rod.
EXAMPLE 11.7
Calculate
the speed of sound in a steel rod whose Young’s modulus Y = 2 × 1011 N m-2 and ρ = 7800 kg m-3.
Solution
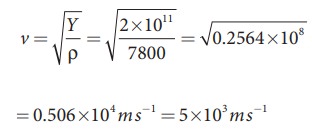
Therefore,
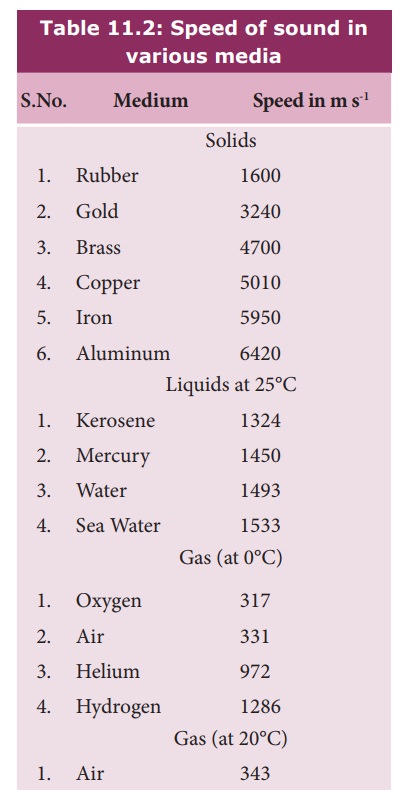
longitudinal waves travel faster in a solid than in a liquid or a gas. Now you
may understand why a shepherd checks before crossing railway track by keeping
his ears on the rails to safegaurd his cattle.
EXAMPLE 11.8
An
increase in pressure of 100 kPa
causes a certain volume of water to decrease by 0.005% of its original volume.
(a)
Calculate the bulk modulus of water?.
(b)
Compute the speed of sound (compressional waves) in water?.
Solution
(a)
Bulk modulus
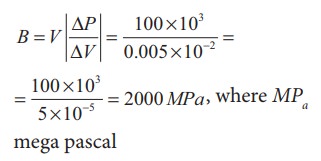
(b)
Speed of sound in water is
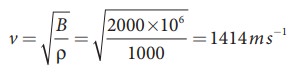
Related Topics