Solved Example Problems for Waves Superposition Principle

EXAMPLE 11.16

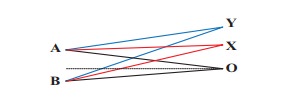
Consider two sources A and B as shown in the figure below. Let the two sources emit simple harmonic waves of same frequency but of different amplitudes, and both are in phase (same phase). Let O be any point equidistant from A and B as shown in the figure. Calculate the intensity at points O, Y and X. (X and Y’ are not equidistant from A & B)

Solution

The distance between OA and OB are the same and hence, the waves starting from A and B reach O after covering equal distances (equal path lengths). Thus, the path difference between two waves at O is zero.

OA âˆ’ OB = 0

Since the waves are in the same phase, at the point O, the phase difference between two waves is also zero. Thus, the resultant intensity at the point O is maximum.

Consider a point Y, such that the path difference between two waves is Î». Then the phase difference at Y is

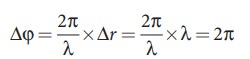
Therefore, at the point Y, the two waves from A and B are in phase, hence, the intensity will be maximum.

Consider a point X, and let the path difference the between two waves be λ/2.

Then the phase difference at X is

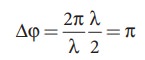
Therefore, at the point X, the waves meet and are in out of phase, Hence, due to destructive interference, the intensity will be minimum.

EXAMPLE 11.17

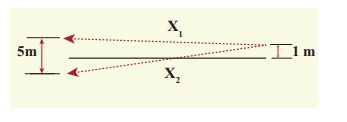
Two speakers C and E are placed 5 m apart and are driven by the same source. Let a man stand at A which is 10 m away from the mid point O of C and E. The man walks towards the point O which is at 1 m (parallel to OC) as shown in the figure. He receives the first minimum in sound intensity at B. Then calculate the frequency of the source.

(Assume speed of sound = 343 m s-1)

Solution

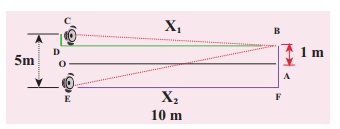
The first minimum occurs when the two waves reaching the point B are 180° (out of phase). The path difference ∆x = λ/2.

In order to calculate the path difference, we have to find the path lengths x1 and x2.

In a right triangle BDC,

The path difference ∆x = x2 âˆ’ x1 = 10.6 m−10.1 m = 0.5 m. Required that this path difference

Formation of beats

EXAMPLE 11.18

Consider two sound waves with wavelengths 5 m and 6 m. If these two waves propagate in a gas with velocity 330 ms-1. Calculate the number of beats per second.

Solution

Given Î»1 = 5m and Î»2 = 6m

Velocity of sound waves in a gas is v = 330 ms-1

The relation between wavelength and velocity is v = Î»f => f = v/λ

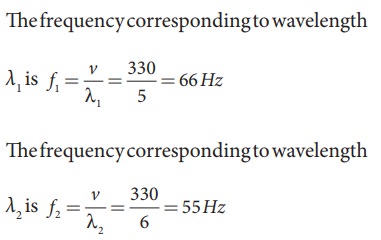
The number of beats per second is

| f1 âˆ’ f2| = |66 − 55| = 11 beats per sec

EXAMPLE 11.19

Two vibrating tuning forks produce waves whose equation is given by y1 = 5 sin(240Ï€ t) and y2 = 4 sin(244Ï€t). Compute the number of beats per second.

Solution

Given y1 = 5 sin(240Ï€ t) and y2 = 4 sin(244Ï€t)

Comparing with y = A sin(2Ï€ f1t), we get

2Ï€f1 = 240Ï€ â‡’ f1 = 120Hz

2Ï€f2 = 244Ï€ â‡’ f2 = 122Hz

The number of beats produced is | f1 âˆ’ f2| = |120 − 122| = |− 2|=2 beats per sec