Physics - Solved Example Problems for Progressive Waves (or) Travelling Waves | 11th Physics : UNIT 11 : Waves
Chapter: 11th Physics : UNIT 11 : Waves
Solved Example Problems for Progressive Waves (or) Travelling Waves
EXAMPLE 11.11
Sketch y = x −a for different values of a.
Solution

This implies, when increasing the value of a, the line shifts towards right side. For a = vt, y = x − vt satisfies the differential equation. Though this function satisfies the differential equation, it is not finite for all values of x and t. Hence, it does not represent a wave.
EXAMPLE 11.12
How does the wave y = sin(x − a) for a = 0, a = π/4, a = π/2, a = 3π/2, a = π look like?. Sketch this wave.
Solution
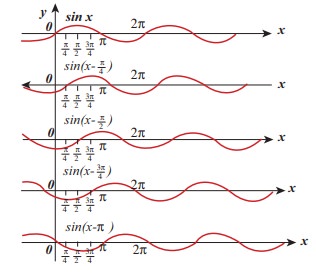
From the above picture we observe that y = sin (x−a) for a = 0, a = π/4, a = π/2, a = 3π/2 and a = π, the function y = sin (x−a) shifts towards right. Further, we can take a = vt and v = π/4 , and sketching for different times t = 0s, t = 1 s, t = 2s etc., we once again observe that y = sin(x−vt) moves towards the right. Hence, y = sin(x−vt) is a travelling (or progressive) wave moving towards the right. If y = sin(x+vt) then the travelling (or progressive) wave moves towards the left. Thus, any arbitrary function of type y = f(x−vt) characterising the wave must move towards right and similarly, any arbitrary function of type y = f(x+vt) characterizing the wave must move towards left.
EXAMPLE 11.13
Check the dimensional of the wave y = sin(x−vt). If it is dimensionally wrong, write the above equation in the correct form.
Solution
Dimensionally it is not correct. we know that y = sin(x−vt) must be a dimensionless quantity but x−vt has dimension. The correct equation is y = sin (k x−ωt), where k and ω have the dimensions of inverse of length and inverse of time respectively. The sine functions and cosine functions are periodic functions with period 2π. Therefore, the correct expression is y = sin ([2π/λ]x, [2π/T]t) where λ and T are wavelength and time period, respectively.
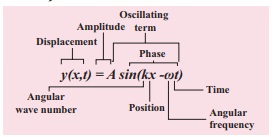
In general, y(x,t)=A sin(k x−ωt).
EXAMPLE 11.14
The wavelength of two sine waves are λ1 = 1m and λ2 = 6m. Calculate the corresponding wave numbers.
Solution
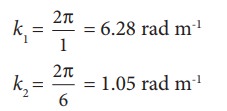
EXAMPLE 11.15
A mobile phone tower transmits a wave signal of frequency 900MHz. Calculate the length of the waves transmitted from the mobile phone tower.
Solution
Frequency, f = 900 MHz = 900 ×106 Hz
The speed of wave is c = 3 × 108m s−1
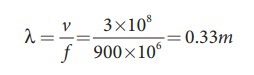
Related Topics