Chapter: 11th Physics : UNIT 11 : Waves
Explanation of stationary waves
Explanation of stationary waves
When the wave hits the rigid boundary it bounces back to the original medium and can interfere with the original waves. A pattern is formed, which are known as standing waves or stationary waves. Consider two harmonic progressive waves (formed by strings) that have the same amplitude and same velocity but move in opposite directions. Then the displacement of the first wave (incident wave) is
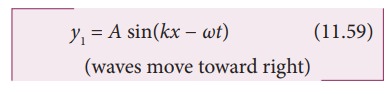
and the displacement of the second wave (reflected wave) is
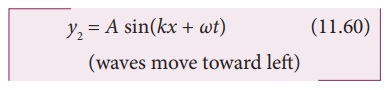
both will interfere with each other by the principle of superposition, the net displacement is

Substituting equation (11.59) and equation (11.60) in equation (11.61), we get

Using trigonometric identity, we rewrite equation (11.62) as
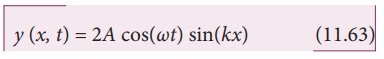
This represents a stationary wave or standing wave, which means that this wave does not move either forward or backward, whereas progressive or travelling waves will move forward or backward. Further, the displacement of the particle in equation (11.63) can be written in more compact form,
y(x,t) = Aʹ cos(ωt)
where, Aʹ = 2Asin(kx), implying that the particular element of the string executes simple harmonic motion with amplitude equals to Aʹ. The maximum of this amplitude occurs at positions for which
sin(kx) =1
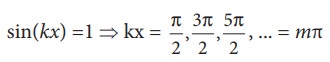
where m takes half integer or half integral values. The position of maximum amplitude is known as antinode. Expressing wave number in terms of wavelength, we can represent the anti-nodal positions as
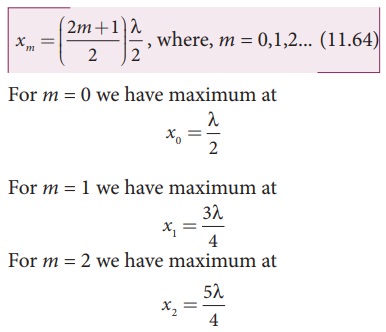
and so on.
The distance between two successive anti-nodes can be computed by
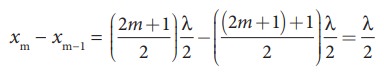
Similarly, the minimum of the amplitude A' also occurs at some points in the space, and these points can be determined by setting
sin(kx)= 0 ⇒ k x = 0,π,2π,3π,… = n π
where n takes integer or integral values. Note that the elements at these points do not vibrate (not move), and the points are called nodes. The nthnodal positions is given by,

For n = 0 we have minimum at
x0 = 0
For n = 1 we have minimum at
x1 = λ /2
For n = 2 we have maximum at
x2 = λ
and so on.
The distance between any two successive nodes can be calculated as
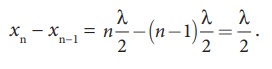
EXAMPLE 11.20
Compute the distance between anti-node and neighbouring node.
Solution
For nth mode, the distance between anti-node and neighbouring node is
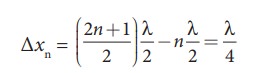
Related Topics