Physics - Solved Example Problems for Stationary waves | 11th Physics : UNIT 11 : Waves
Chapter: 11th Physics : UNIT 11 : Waves
Solved Example Problems for Stationary waves
EXAMPLE 11.20
Compute the distance between anti-node and neighbouring node.
Solution
For nth mode, the distance between anti-node and neighbouring node is
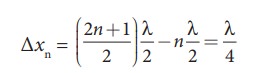
EXAMPLE 11.21
Let f be the fundamental frequency of the string. If the string is divided into three segments l1, l2 and l3 such that the fundamental frequencies of each segments be f1, f2 and f3, respectively. Show that
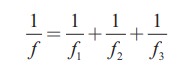
Solution
For a fixed tension T and mass density µ, frequency is inversely proportional to the string length i.e.

EXAMPLE 11.22
Consider a string in a guitar whose length is 80 cm and a mass of 0.32 g with tension 80 N is plucked. Compute the first four lowest frequencies produced when it is plucked.
Solution
The velocity of the wave
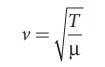
The length of the string, L = 80 cm=0.8 m The mass of the string, m = 0.32 g = 0.32 × 10-3kg
Therefore, the linear mass density,
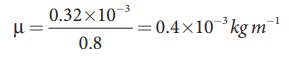
The tension in the string, T = 80 N
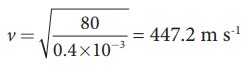
The wavelength corresponding to the fundamental frequency f1 is λ1 = 2L = 2 × 0.8 = 1.6 m
The fundamental frequency f1 corresponding to the wavelength λ1
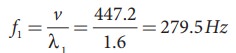
Similarly, the frequency corresponding to the second harmonics, third harmonics and fourth harmonics are
f2 = 2f1 = 559 Hz
f3 = 3f1 = 838.5 Hz
f4 = 4f1 = 1118 Hz
Related Topics