Solved Example Problems for Vibrations of Air Column

EXAMPLE 11.25

If a flute sounds a note with 450Hz , what are the frequencies of the second, third, and fourth harmonics of this pitch?. If the clarinet sounds with a same note as 450Hz, then what are the frequencies of the lowest three harmonics produced ?.

Solution

For a flute which is an open pipe, we have

Second harmonics          f2 = 2 f1 = 900 Hz

Third harmonics   f3 = 3 f1        = 1350 Hz

Fourth harmonics f4 = 4 f1        = 1800 Hz

For a clarinet which is a closed pipe, we have

Second harmonics          f 2 = 3 f1      = 1350 Hz

Third harmonics   f 3 = 5 f1       = 2250 Hz

Fourth harmonics f 4 = 7 f1       = 3150 Hz

EXAMPLE 11.26

If the third harmonics of a closed organ pipe is equal to the fundamental frequency of an open organ pipe, compute the length of the open organ pipe if the length of the closed organ pipe is 30 cm.

Solution

Let l2 be the length of the open organ pipe, with l1 =30 cm the length of the closed organ pipe.

It is given that the third harmonic of closed organ pipe is equal to the fundamental frequency of open organ pipe.

The third harmonic of a closed organ pipe is

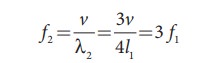
The fundamental frequency of open organ pipe is

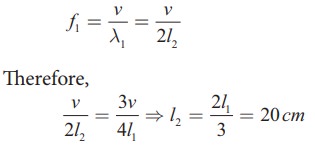
EXAMPLE 11.27

A frequency generator with fixed frequency of 343 Hz is allowed to vibrate above a 1.0 m high tube. A pump is switched on to fill the water slowly in the tube. In order to get resonance, what must be the minimum height of the water?. (speed of sound in air is 343 m s−1)

Solution

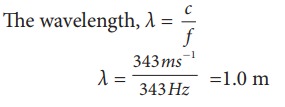
Let the length of the resonant columns be L1, L2 and L3. The first resonance occurs at length L1

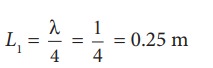
The second resonance occurs at length L2

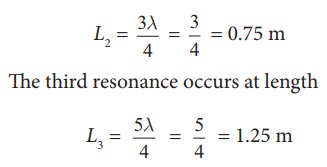
and so on.

Since total length of the tube is 1.0 m the third and other higher resonances do not occur. Therefore, the minimum height of water Hmin for resonance is,

Hmin = 1.0 m − 0.75 m = 0.25 m

EXAMPLE 11.28

A student performed an experiment to determine the speed of sound in air using the resonance column method. The length of the air column that resonates in the fundamental mode with a tuning fork is 0.2 m. If the length is varied such that the same tuning fork resonates with the first overtone at 0.7 m. Calculate the end correction.

Solution

End correction

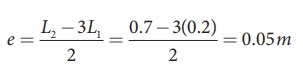
EXAMPLE 11.29

Consider a tuning fork which is used to produce resonance in an air column. A resonance air column is a glass tube whose length can be adjusted by a variable piston. At room temperature, the two successive resonances observed are at 20 cm and 85 cm of the column length. If the frequency of the length is 256 Hz, compute the velocity of the sound in air at room temperature.

Solution

Given two successive length (resonance) to be L1 = 20 cm and L2 = 85 cm

The frequency is f = 256 Hz

v = f λ = 2f∆L = 2f (L2 âˆ’ L1)

= 2 × 256 × (85 − 20) × 10−2 m s−1

v= 332.8 cm−1