Chapter: 11th Physics : UNIT 11 : Waves
Doppler Effect
DOPPLER
EFFECT
Often
we have noticed that the siren sound coming from a police vehicle or ambulance
increases when it comes closer to us and decreases when it moves away from us.
When we stand near any passing train the train whistle initially increases and
then it will decrease. This is known as Doppler Effect, named after Christian
Doppler (1803 – 1853). Suppose a source produces sound with some frequency, we
call it the as source frequency fs.
If the source and an observer are at a fixed distance then the observer
observes the sound with frequency f0.
This is the same as the sound frequency produced by the source fs, i.e., f0 = fs. Hence, there is no difference in frequency, implying
no Doppler effect is observed.

What
happens if either source or an observer or both move?. Certainly, fo ≠ fs. That is, when the source and the observer are in
relative motion with respect to each other and to the medium in which sound
propagates, the frequency of the sound wave observed is different from the
frequency of the source. This phenomenon is called Doppler Effect. The
frequency perceived by the observer is known as apparent frequency. We can
consider the following situations for the study of Doppler effect in sound
waves
(a) Source and Observer: We can consider either the source or observer in motion or both are in motion.
Further we can treat the motion to be along the line joining the source and the
observer, or inclined at an angle θ to this line.
(b) Medium: We can treat the medium to be stationary or the direction of
motion of the medium is along or opposite to the direction of propagation of
sound.
(c) Speed of Sound: We can also consider the case where speed of the source or
an observer is greater or lesser than the speed of sound.
In
the following section, we make the following assumptions: the medium is
stationary, and motion is along the line joining the source and the observer,
and the speeds of the source and the observer are both less than the speed of
sound in that medium.
We
consider three cases:
(i)
Source in motion and Observer is at rest.
(a) Source moves towards
observer
(b) Source moves away from
the observer
(ii) Observer in motion and Source is at rest.
(a) Observer moves towards
Source
(b) Observer receding away
from the Source
(iii)
Both are in motion
(a) Source and Observer
approach each other
(b) Source and Observer
recede from
each other
(c) Source chases Observer
(d) Observer chases Source
Stationary
observer and stationary source means the observer and source are both at rest with respect to medium
respectively
Source in motion and the observer at rest
(a) Source moves towards the observer
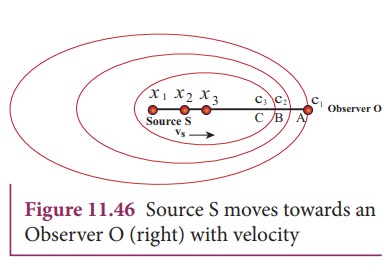
Suppose
a source S moves to the right (as shown in Figure 11.46) with a velocity vs and let the frequency of
the sound waves produced by the source be fs.
We assume the velocity of sound in a medium is v. The compression (sound wave front) produced by the source S at
three successive instants of time are shown in the Figure 11.46. When S is at
position x1 the
compression is at C1. When
S is at position x2, the
compression is at C2 and
similarly for x3 and C3. Assume that if C1 reaches the observer’s position
A then at that instant C2
reaches the point B and C3 reaches the point C as shown in the Figure 11.46.
It is obvious to see that the distance between compressions C2 and C3 is shorter than distance between C1 and C2.
This means the wavelength decreases when the source S moves towards the
observer O (since sound travels longitudinally and wavelength is the distance
between two consecutive compressions). But frequency is inversely related to
wavelength and therefore, frequency increases.
Let
λ be the wavelength of the source S
as measured by the observer when S is at position x1 and λʹ be
wavelength of the source observed by the observer when S moves to position x2. Then the change in
wavelength is ∆λ = λ− λʹ = vst, where t is the time taken by the source to
travel between x1 and x2. Therefore,

On
substituting equation (11.84) in equation (11.83), we get
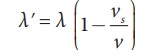
Since
frequency is inversely proportional to wavelength, we have
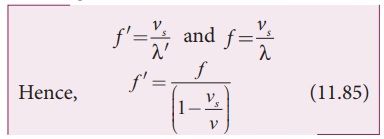
Since,
vs/v << 1, we use the binomial expansion and retaining only
first order in vs/v , we get

(b) Source moves away from the observer:
Since
the velocity here of the source is opposite in direction when compared to case
(a), therefore, changing the sign of the velocity of the source in the above
case i.e, by substituting (vs→ −vs )
in equation (11.83), we get

Observer in motion and source at rest
(a) Observer moves towards Source
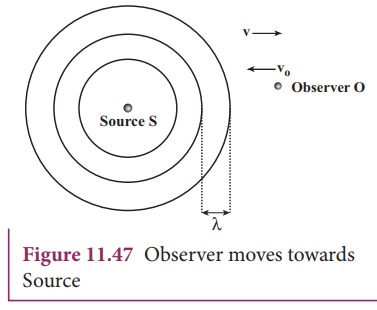
Let
us assume that the observer O moves towards the source S with velocity vo. The source S is at rest
and the velocity of sound waves (with respect to the medium) produced by the
source is v. From the Figure 11.47,
we observe that both vo
and v are in opposite direction.
Then, their relative velocity is vr = v + v0.
The wavelength of the sound wave is λ = v/f, which means the frequency observed
by the observer O is f ′ = vr/λ . Then
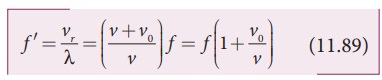
(b) Observer recedes away from the Source
If the observer O is moving away (receding away) from the source S, then velocity v0 and v moves in the same direction. Therefore, their relative velocity is vr = v − v0. Hence, the frequency observed by the observer O is
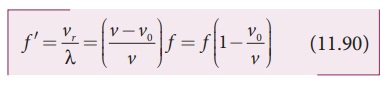
Both are in motion
(a) Source and observer approach each other

Let
vs and v0 be the respective
velocities of source and observer approaching each other as shown in Figure
11.48. In order to calculate the apparent frequency observed by the observer,
as a simple calculation, let us have a dummy (behaving as observer or source)
in between the source and observer. Since the dummy is at rest, the dummy
(observer) observes the apparent frequency due to approaching source as given
in equation (11.85) as
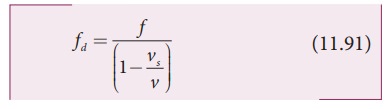
At
that instant of time, the true observer approaches the dummy from the other
side. Since the source (true source) comes in a direction opposite to true
observer, the dummy (source) is treated as stationary source for the true
observer at that instant. Hence, apparent frequency when the true observer
approaches the stationary source (dummy source), from equation (11.89) is

Since
this is true for any arbitrary time, therefore, comparing equation (11.91) and
equation (11.92), we get

Hence,
the apparent frequency as seen by the observer is
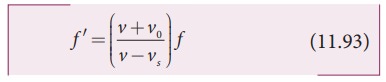
(b) Source and observer recede from each other

Here,
we can derive the result as in the previous case. Instead of a detailed
calculation, by inspection from Figure 11.49, we notice that the velocity of
the source and the observer each point in opposite directions with respect to
the case in (a) and hence, we substitute (vs
→ −vs)
and (v0 → −v0)
in equation (11.93), and therefore, the apparent frequency observed by the
observer when the source and observer recede from each other is
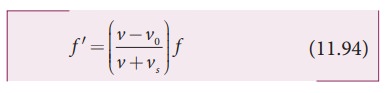
(c) Source chases the observer

Only
the observer’s velocity is oppositely directed when compared to case (a).
Therefore, substituting (v0
→ −v0)
in equation (11.93), we get
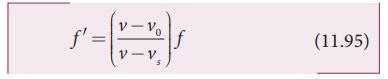
(d) Observer chases the
source

Only
the source velocity is oppositely directed when compared to case (a).
Therefore, substituting vs
→ −vs in
equation (11.93), we get
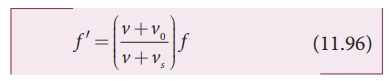
Applications of Doppler effect
Doppler effect has many applications. Specifically Doppler effect in light has many applications in astronomy.
As an example, while observing the spectra from distant objects
like stars or galaxies, it is possible to determine the velocities at which
distant objects like stars or galaxies move towards or away from Earth. If the
spectral lines of the star are found to shift towards red end of the spectrum
(called as red shift) then the star is receding away from the Earth. Similarly,
if the spectral lines of the star are found to shift towards the blue end of
the spectrum (called as blue shift) then the star is approaching Earth.
Let
∆λ be the Doppler shift. Then ∆λ= v/c
λ, where v is the velocity of the star. It may be noted that Doppler shift
measures only the radial component (along the line of sight) of the relative
velocity v.
EXAMPLE 11.30
A
sound of frequency 1500 Hz is emitted by a source which moves away from an
observer and moves towards a cliff at a speed of 6 ms-1.
(a)
Calculate the frequency of the sound which is coming directly from the source.
(b)
Compute the frequency of sound heard by the observer reflected off the cliff.
Assume the speed of sound in air is 330 m s-1
Solution
(a)
Source is moving away and observer is stationary, therefore, the frequency of
sound heard directly from source is

(b)
Sound is reflected from the cliff and reaches observer, therefore,
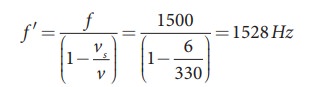
EXAMPLE 11.31
An
observer observes two moving trains, one reaching the station and other leaving
the station with equal speeds of 8 m s−1. If each train sounds its
whistles with frequency 240 Hz, then calculate the number of beats heard by the
observer.
Solution:
Observer
is stationary
(i)
Source (train) is moving towards an observer:
Apparent
frequency due to train arriving station is
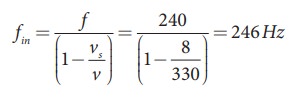
(ii)
Source (train) is moving away form an observer:
Apparent
frequency due to train leaving station is
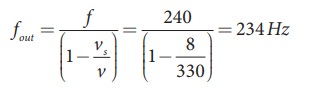
So
the number of beats = | fin
-fout| = (246-234) = 12
Related Topics