Chapter: 11th Physics : UNIT 11 : Waves
Particle velocity and Progressive wave velocity
Particle velocity and wave velocity
In a plane progressive harmonic wave, the constituent particles in the medium oscillate simple harmonically about their equilibrium positions. When a particle is in motion, the rate of change of displacement at any instant of time is defined as velocity of the particle at that instant of time. This is known as particle velocity.
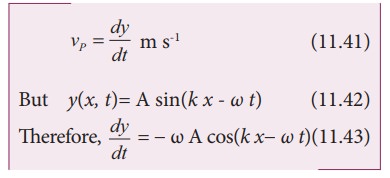
Similarly, we can define velocity (here speed) for the travelling wave (or progressive wave). In order to determine the velocity of a progressive wave, let us consider a progressive wave (shown in Figure 11.23) moving towards right. This can be mathematically represented as a sinusoidal wave. Let P be any point on the phase of the wave and yP be its displacement with respect to the mean position. The displacement of the wave at an instant t is
y = y(x,t) = A sin(k x− ω t)
At the next instant of time tʹ = t + ∆t the position of the point P is xʹ = x + ∆x. Hence, the displacement of the wave at this instant is
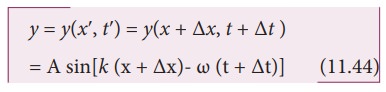
Since the shape of the wave remains the same, this means that the phase of the wave remains constant (i.e., the y- displacement of the point is a constant). Therefore, equating equation (11.42) and equation (11.44), we get
y(x',t') = y(x,t), which implies
A sin[k (x + ∆x)− ω (t + ∆t)]= A sin(k x− ω t)
Or
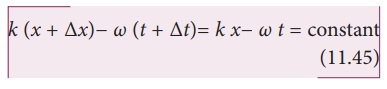
On simplification of equation (11.45), we get
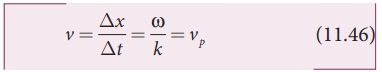
where vp is called wave velocity or phase velocity.
By expressing the angular frequency and wave number in terms of frequency and wave length, we obtain
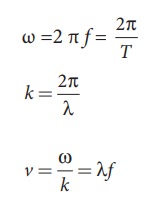
EXAMPLE 11.15
A mobile phone tower transmits a wave signal of frequency 900MHz. Calculate the length of the waves transmitted from the mobile phone tower.
Solution
Frequency, f = 900 MHz = 900 ×106 Hz
The speed of wave is c = 3 × 108m s−1
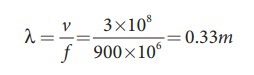
Related Topics