Fundamental frequency and overtones

Fundamental frequency and overtones

Let us now keep the rigid boundaries at x = 0 and x = L and produce a standing waves by wiggling the string (as in plucking strings in a guitar). Standing waves with a specific wavelength are produced. Since, the amplitude must vanish at the boundaries, therefore, the displacement at the boundary must satisfy the following conditions

y(x = 0, t) = 0 and y(x = L, t) = 0      (11.68)

Since the nodes formed are at a distance λn/2 apart, we have n(λn/2) = L, where n is an integer, L is the length between the two boundaries and λn is the specific wavelength that satisfy the specified boundary conditions. Hence,

Therefore, not all wavelengths are allowed. The (allowed) wavelengths should fit with the specified boundary conditions, i.e., for n = 1, the first mode of vibration has specific wavelength Î»l = 2L. Similarly for n = 2, the second mode of vibration has specific wavelength

For n = 3, the third mode of vibration has specific wavelength

and so on.

The frequency of each mode of vibration (called natural frequency) can be calculated.

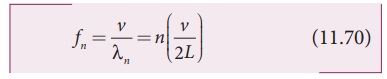
The lowest natural frequency is called the fundamental frequency.

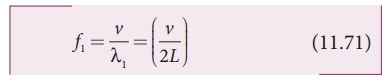
The second natural frequency is called the first over tone.

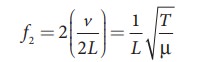
The third natural frequency is called the second over tone.

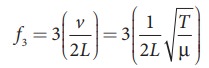
Therefore, the nth natural frequency can be computed as integral (or integer ) multiple of fundamental frequency, i.e.,

fn = nf1,      where n is an integer (11.72)

If natural frequencies are written as integral multiple of fundamental frequencies, then the frequencies are called harmonics. Thus, the  first harmonic is f1 = f1 (the fundamental frequency is called first harmonic), the second harmonic is f2 = 2f1, the third harmonic is f3 = 3f1 etc.

EXAMPLE 11.22

Consider a string in a guitar whose length is 80 cm and a mass of 0.32 g with tension 80 N is plucked. Compute the first four lowest frequencies produced when it is plucked.

Solution

The velocity of the wave

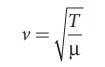
The length of the string, L = 80 cm=0.8 m The mass of the string, m = 0.32 g = 0.32 × 10-3kg

Therefore, the linear mass density,

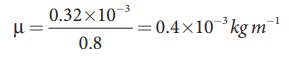
The tension in the string, T = 80 N

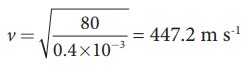
The wavelength corresponding to the fundamental frequency f1 is Î»1 = 2L = 2 × 0.8 = 1.6 m

The fundamental frequency f1 corresponding to the wavelength Î»1

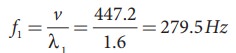
Similarly, the frequency corresponding to the second harmonics, third harmonics and fourth harmonics are

f2 = 2f1 = 559 Hz

f3 = 3f1 = 838.5 Hz

f4 = 4f1 = 1118 Hz