Chapter: 11th Physics : UNIT 11 : Waves
Progressive Waves (or) Travelling Waves
PROGRESSIVE
WAVES (OR) TRAVELLING WAVES
If
a wave that propagates in a medium is continuous then it is known as
progressive wave or travelling wave.
Characteristics of progressive waves
2.
The phase of every particle ranges from 0 to 2π.
3.
No particle remains at rest permanently. During wave propagation, particles
come to the rest position only twice at the extreme points.
4.
Transverse progressive waves are characterized by crests and troughs whereas
longitudinal progressive waves are characterized by compressions and
rarefactions.
5.
When the particles pass through the mean position they always move with the
same maximum velocity.
6.
The displacement, velocity and acceleration of particles separated from each
other by nλ are the same, where n is an integer, and λ is the
wavelength.
Equation of a plane progressive wave
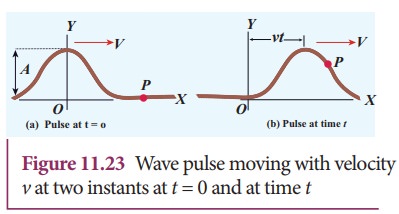
Suppose
we give a jerk on a stretched string at time t = 0s. Let us assume
that the wave pulse created during this disturbance moves along positive x direction with constant speed v as shown in Figure 11.23 (a). We can
represent the shape of the wave pulse, mathematically as y = y(x, 0) = f(x) at time t = 0s.
Assume that the shape of the wave pulse remains the same during the propagation.
After some time t, the pulse moving
towards the right and any point on it can be represented by x' (read it as x prime) as shown in Figure 11.23 (b). Then,
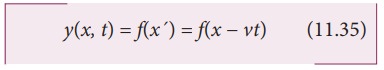
Similarly,
if the wave pulse moves towards left with constant speed v, then y = f(x
+ vt). Both waves y = f(x + vt)
and y = f(x − vt) will satisfy the following one
dimensional differential equation known as the wave equation
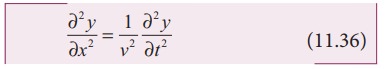
where
the symbol ∂ represent partial (read ∂y/∂x as partial y by partial x). Not all
the solutions satisfying this differential equation can represent waves,
because any physical acceptable wave must take finite values for all values of
x and t. But if the function represents a wave then it must satisfy the
differential equation. Since, in one dimension (one independent variable), the
partial derivative with respect to x is the same as total derivative in
coordinate x, we write
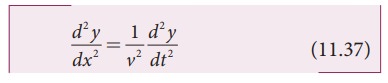
This
can be extended to more than one dimension (two, three, etc.). Here, for
simplicity, we focus only on the one dimensional wave equation.
EXAMPLE 11.11
Sketch
y = x −a for different values
of a.
Solution

This
implies, when increasing the value of a,
the line shifts towards right side. For a
= vt, y = x − vt satisfies the differential equation. Though this function
satisfies the differential equation, it is not finite for all values of x and t. Hence, it does not represent a wave.
EXAMPLE 11.12
How
does the wave y = sin(x − a)
for a = 0, a = π/4, a = π/2, a =
3π/2, a = π look like?. Sketch this wave.
Solution
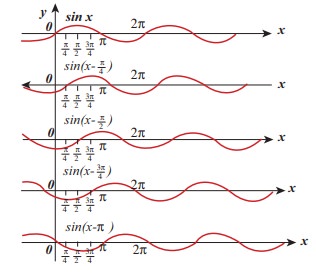
From
the above picture we observe that y = sin
(x−a) for a = 0, a = π/4, a = π/2, a = 3π/2 and a = π, the function y = sin
(x−a) shifts towards right. Further, we can take a = vt and v = π/4 , and
sketching for different times t = 0s, t
= 1 s, t = 2s etc., we once
again observe that y = sin(x−vt)
moves towards the right. Hence, y =
sin(x−vt) is a travelling (or progressive) wave moving towards the right.
If y = sin(x+vt) then the travelling
(or progressive) wave moves towards the left. Thus, any arbitrary function of
type y = f(x−vt) characterising the wave must
move towards right and similarly, any arbitrary function of type y = f(x+vt)
characterizing the wave must move towards left.
EXAMPLE 11.13
Check
the dimensional of the wave y = sin(x−vt).
If it is dimensionally wrong, write the above equation in the correct form.
Solution
Dimensionally
it is not correct. we know that y =
sin(x−vt) must be a dimensionless quantity but x−vt has dimension. The
correct equation is y = sin (k x−ωt),
where k and ω have the dimensions of inverse of length and inverse of time respectively. The sine functions and
cosine functions are periodic functions with period 2π. Therefore, the correct
expression is y = sin ([2π/λ]x, [2π/T]t) where λ and T are wavelength and time
period, respectively.
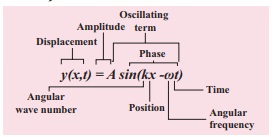
In
general, y(x,t)=A sin(k x−ωt).
Graphical representation of the wave
Let
us graphically represent the two forms of the wave variation
(a)
Space (or
Spatial) variation graph
(b)
Time (or
Temporal) variation graph
(a) Space variation graph
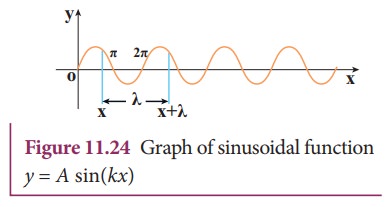
By
keeping the time fixed, the change in displacement with respect to x is plotted. Let us consider a
sinusoidal graph, y = A sin(kx) as shown in the Figure 11.24, where k is a constant. Since the wavelength λ denotes the distance between any two points in the same state of
motion, the displacement y is the
same at both the ends y = x and y = x + λ, i.e.,
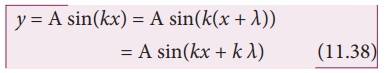
The
sine function is a periodic function with period 2π. Hence,
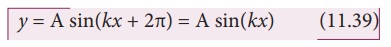
Comparing
equation (11.38) and equation (11.39), we get
kx +
k λ = kx + 2π
This
implies

where
k is called wave number. This
measures how many wavelengths are present in 2π radians.
The
spatial periodicity of the wave is
Then,
At
t = 0 s y(x, 0) = y(x + λ, 0)
and
At
any time t, y(x, t) = y(x + λ, t)
EXAMPLE 11.14
The
wavelength of two sine waves are λ1 = 1m and λ2 = 6m.
Calculate the corresponding wave
numbers.
Solution
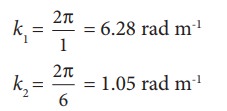
(b) Time variation graph
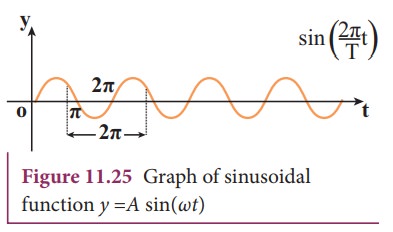
By
keeping the position fixed, the change in displacement with respect to time is
plotted. Let us consider a sinusoidal graph, y =A sin(ωt) as shown in the Figure 11.25, where ω is angular frequency of the wave which measures how quickly wave
oscillates in time or number of cycles per second.
The
temporal periodicity or time period is
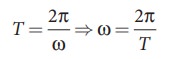
The
angular frequency is related to frequency f
by the expression ω = 2 πf, where the frequency f is defined as the number of oscillations
made by the medium particle per second. Since inverse of frequency is time
period, we have,
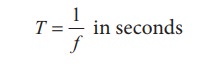
This
is the time taken by a medium particle to complete one oscillation. Hence, we
can define the speed of a wave (wave speed, v)
as the distance traversed by the wave per second
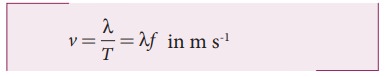
which
is the same relation as we obtained in equation (11.4).
Particle
velocity and wave velocity
In
a plane progressive harmonic wave, the constituent particles in the medium
oscillate simple harmonically about their equilibrium positions. When a
particle is in motion, the rate of change of displacement at any instant of
time is defined as velocity of the particle at that instant of time. This is
known as particle velocity.
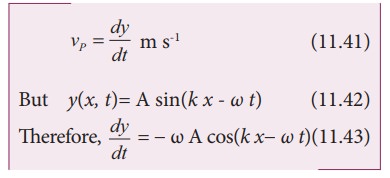
Similarly,
we can define velocity (here speed) for the travelling wave (or progressive
wave). In order to determine the velocity of a progressive wave, let us
consider a progressive wave (shown in Figure 11.23) moving towards right. This
can be mathematically represented as a sinusoidal wave. Let P be any point on
the phase of the wave and yP
be its displacement with respect to the mean position. The displacement of the
wave at an instant t is
y = y(x,t) = A sin(k x− ω t)
At
the next instant of time tʹ = t + ∆t
the position of the point P is xʹ = x
+ ∆x. Hence, the displacement of the
wave at this instant is
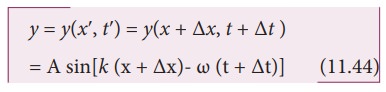
Since
the shape of the wave remains the same, this means that the phase of the wave
remains constant (i.e., the y-
displacement of the point is a constant). Therefore, equating equation (11.42)
and equation (11.44), we get
y(x',t') =
y(x,t), which implies
A
sin[k (x + ∆x)− ω (t
+ ∆t)]= A sin(k x− ω t)
Or
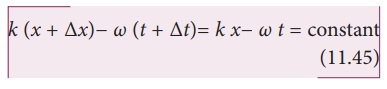
On
simplification of equation (11.45), we get
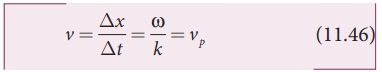
where
vp is called wave velocity or phase velocity.
By
expressing the angular frequency and wave number in terms of frequency and wave
length, we obtain
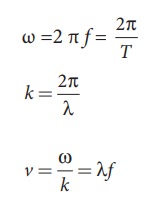
EXAMPLE 11.15
A
mobile phone tower transmits a wave signal of frequency 900MHz. Calculate the
length of the waves transmitted from the mobile phone tower.
Solution
Frequency,
f = 900 MHz = 900 ×106 Hz
The
speed of wave is c = 3 × 108m
s−1
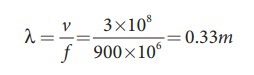
Related Topics