Book Back Numerical Problems

1. The speed of a wave in a certain medium is 900 m/s. If 3000 waves passes over a certain point of the medium in 2 minutes, then compute its wavelength?.

Solution

The speed of a wave in medium v = 900 ms-1

Freq. of wave = no. of waves passing per sec (n) = 3000 waves/2min = 3000 / 2×60 = 25s

Wave length = λ =?

v = n λ

λ  = v/n

A = 900/25 =36m

A = 36m

Answer : λ = 36 m

 

2. Consider a mixture of 2 mol of helium and 4 mol of oxygen. Compute the speed of sound in this gas mixture at 300 K.

Solution

Helium - 2 mole, oxygen - 4 mol

He & O2 are mixed, hence molecular weight of the mixture of gases

Answer : 400.9 ms-1

 

3. A ship in a sea sends SONAR waves straight down into the seawater from the bottom of the ship. The signal reflects from the deep bottom bed rock and returns to the ship after 3.5 s. After the ship moves to 100 km it sends another signal which returns back after 2s. Calculate the depth of the sea in each case and also compute the difference in height between two cases.

Solution

Velocity of SONAR waves in water C = 1500 ms-1

Time taken by be wave after reflection from the bottom of sea

2t = 3.5s

t =1.75s

Distance covered (d) = ?

C = d/t => d = c.t = 1500 × 1.75 - 2625 m

After moving 100km

The time taken by the wave = 2t = 2s

T  = 2/2 = 1s

d =?

d = 1500 × l

= 1500

The different between these two heights . = 2625 - 1500

= 1125m

Answer : Δd = 1149.75 m

 

4. A sound wave is transmitted into a tube as shown in figure. The sound wave splits into two waves at the point A which recombine at point B. Let R be the radius of the semi-circle which is varied until the first minimum. Calculate the radius of the semi-circle if the wavelength of the sound is 50.0 m.

Answer : R = 21.9 m

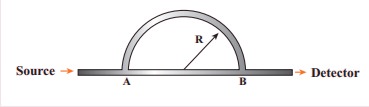
Solution

Consider the sound waves start from the pt A. The sound waves will meet at the picture B & interfere and can be detected.

The path length of sound waves passing through the curve is equal to half the circle having radio centered at c.

Thus, be path length of be sound waves in curve part is

L1 = πγ

The path length of the sound in tube ABC is equal to the diameter of the circle having radius γ centered at e.

So the path length of the sound waves travelling in it = L2 =2r

The path difference of the sound waves at the picture is

ΔP = L1 - L2

= πr— 2r

ΔP = r(π - 2) ...(1)

For the sound to be heard minimum at the detected the difference in path length of be sound waves is

ΔP = λ/2    …………(2)

From equation (1)

r(π- 2) = λ/2

wavelength of sound = λ = 50m

radius of be semicircle r = ?

r = 50 / [2 × 3.14 – 4] = 50/2.28

r = 21.9m

Answer : R = 21.9 m

 

5.   N tuning forks are arranged in order of increasing frequency and any two successive tuning forks give n beats per second when sounded together. If the last fork gives double the frequency of the first (called as octave), Show that the frequency of the first tuning fork is f = (N−1)n.

Solution

No.of tuning forks = N

The frequency of the first is double to be last

The difference of frequency for two successive tuning forks NHz

Let be frequency of the first tuning fork is f

Then be frequency of the last tuning fork is f(N-l)n

frequency is reduced to are fourth

flast = - f /2 

an = a + (n-1)d

(i.e.) 2f  =  f + (N-1)n

= (N-1)n

f = (N-1)n

 

6.   Let the source propagate a sound wave whose intensity at a point (initially) be I. Suppose we consider a case when the amplitude of the sound wave is doubled and the frequency is reduced to one-fourth. Calculate now the new intensity of sound at the same point ?.

Solution

Intensity of sound wave  = Iold

Amplitude is doubled = 2A = Anew

Frequency is produced to are fourth

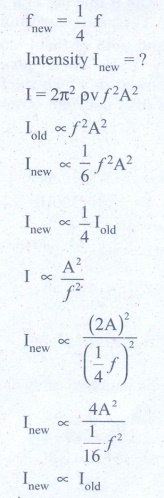
Answer: Inew ∝ ¼ I old

 

7. Consider two organ pipes of same length in which one organ pipe is closed and another organ pipe is open. If the fundamental frequency of closed pipe is 250 Hz. Calculate the fundamental frequency of the open pipe.

Answer: 500Hz

 

8. A police in a siren car moving with a velocity 20 ms-1 chases a thief who is moving in a car with a velocity v0ms-1. The police car sounds atfrequency 300Hz, and both of them move towards a stationary siren of frequency 400Hz. Calculate the speed in which thief is moving.

Solution

The velocity of car = 20ms-1

The frequency of car = 300Hz

The frequency stationary siren = 400Hz

The speed in which thief moving = ?

Answer: vthief = 10 m s-1

 

9. Consider the following function

(a) y = x2 + 2 α t x

(b) y = (x + vt)2

which among the above function can be characterized as a wave ?.

Solution

(a) y = x2 + 2 a t x

It is not describing wave.

(b) y = (x + 2 vx)2

It satisfies wave equation.

Answer: (a) function is not describing wave (b) satisfies wave equation.