Waves Superposition Principle

SUPERPOSITION PRINCIPLE

When a jerk is given to a stretched string which is tied at one end, a wave pulse is produced and the pulse travels along the string. Suppose two persons holding the stretched string on either side give a jerk simultaneously, then these two wave pulses move towards each other, meet at some point and move away from each other with their original identity. Their behaviour is very different only at the crossing/meeting points; this behaviour depends on whether the two pulses have the same or different shape as shown in Figure 11.26.

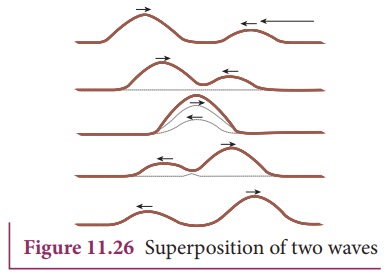
When the pulses have the same shape, at the crossing, the total displacement is the algebraic sum of their individual displacements and hence its net amplitude is higher than the amplitudes of the individual pulses. Whereas, if the two pulses have same amplitude but shapes are 180° out of phase at the crossing point, the net amplitude vanishes at that point and the pulses will recover their identities after crossing. Only waves can possess such a peculiar property and it is called superposition of waves. This means that the principle of superposition explains the net behaviour of the waves when they overlap. Generalizing to any number of waves i.e, if two are more waves in a medium move simultaneously, when they overlap, their total displacement is the vector sum of the individual displacements. We know that the waves satisfy the wave equation which is a linear second order homogeneous partial differential equation in both space coordinates and time. Hence, their linear combination (often called as linear superposition of waves) will also satisfy the same differential equation.

To understand mathematically, let us consider two functions which characterize the displacement of the waves, for example,

y₁ = A₁ sin(kx − ωt)

and

y₂ = A₂ cos(kx − ωt)

Since, both y₁ and y₂ satisfy the wave equation (solutions of wave equation) then their algebraic sum

y = y₁ + y₂

also satisfies the wave equation. This means, the displacements are additive. Suppose we multiply y₁ and y₂ with some constant then their amplitude is scaled by that constant

Further, if C₁ and C₂ are used to multiply the displacements y₁ and y₂, respectively, then, their net displacement y is

y = C₁ y₁ + C₂ y₂

This can be generalized to any number of waves. In the case of n such waves in more than one dimension the displacements are written using vector notation.

Here, the net displacement 

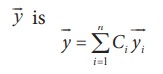
The principle of superposition can explain the following :

(a) Space (or spatial) Interference (also known as Interference)

(b) Time (or Temporal) Interference (also known as Beats)

(c) Concept of stationary waves

Waves that obey principle of superposition are called linear waves (amplitude is much smaller than their wavelengths). In general, if the amplitude of the wave is not small then they are called non-linear waves. These violate the linear superposition principle, e.g. laser. In this chapter, we will focus our attention only on linear waves.

We will discuss the following in different subsections:

Interference of waves

Interference is a phenomenon in which two waves superimpose to form a resultant wave of greater, lower or the same amplitude.

Consider two harmonic waves having identical frequencies, constant phase difference φ and same wave form (can be treated as coherent source), but having amplitudes A₁ and A₂, then

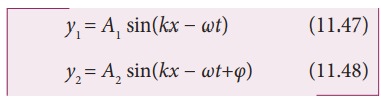
Suppose they move simultaneously in a particular direction, then interference occurs (i.e., overlap of these two waves). Mathematically

Therefore, substituting equation (11.47) and equation (11.48) in equation (11.49), we get

y = A₁ sin(kx − ωt) + A₂ sin(kx − ωt + φ)

Using trigonometric identity sin (α+β) = (sin α cosβ + cosα sinβ ), we get

y = A₁ sin(kx − ωt)+A₂ [sin(kx − ωt) cosφ + cos(kx − ωt) sinφ]

then equation (11.50) can be rewritten as y = A sin(kx−ωt) cosθ + A cos(kx−ωt) sinθ

Since, intensity is square of the amplitude (I = A²), we have

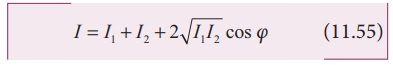
This means the resultant intensity at any point depends on the phase difference at that point.

(a)  For constructive interference:

When crests of one wave overlap with crests of another wave, their amplitudes will add up and we get constructive interference. The resultant wave has a larger amplitude than the individual waves as shown in Figure 11.29 (a).

The constructive interference at a point occurs if there is maximum intensity at that point, which means that

cosφ = + 1 ⇒ φ = 0, 2π,4π,… = 2nπ,

where n = 0,1,2,...

This is the phase difference in which two waves overlap to give constructive interference.

Therefore, for this resultant wave,

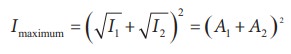
Hence, the resultant amplitude

A= A₁ + A₂

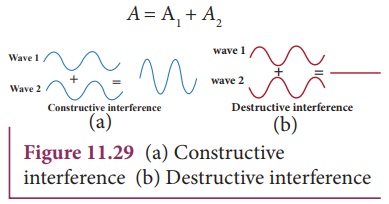
(b) For destructive interference:

When the trough of one wave overlaps with the crest of another wave, their amplitudes “cancel” each other and we get destructive interference as shown in Figure 11.29 (b). The resultant amplitude is nearly zero. The destructive interference occurs if there is minimum intensity at that point, which means cosφ = − 1 ⇒ φ = π,3π,5π,… = (2 n-1) π, where n = 0,1,2,…. i.e. This is the phase difference in which two waves overlap to give destructive interference. Therefore,

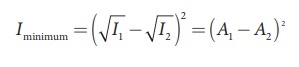
Hence, the resultant amplitude

A=|A₁−A₂|

Let us consider a simple instrument to demonstrate the interference of sound waves as shown in Figure 11.30.

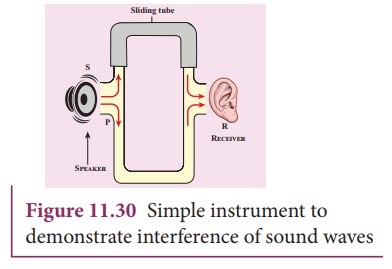
A sound wave from a loudspeaker S is sent through the tube P. This looks like a T-shaped junction. In this case, half of the sound energy is sent in one direction and the remaining half is sent in the opposite direction. Therefore, the sound waves that reach the receiver R can travel along either of two paths. The distance covered by the sound wave along any path from the speaker to receiver is called the path length . From the Figure 11.30, we notice that the lower path length is fixed but the upper path length can be varied by sliding the upper tube i.e., is varied. The difference in path length is known as path difference,

∆r = |r₂ − r₁|

Suppose the path difference is allowed to be either zero or some integer (or integral) multiple of wavelength λ. Mathematically, we have

∆r = nλ                 where, n = 0, 1, 2, 3,....

Then the two waves arriving from the paths r₁ and r₂ reach the receiver at any instant are in phase (the phase difference is 0° or 2π) and interfere constructively as shown in Figure 11.31.

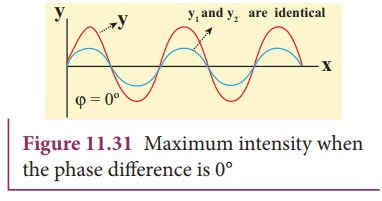
Therefore, in this case, maximum sound intensity is detected by the receiver. If the path difference is some half-odd-integer (or half-integral) multiple of wavelength λ, mathematically, Δ r = n(λ/2)

where, n = 1,3,...            (n is odd)

then the two waves arriving from the paths r₁ and r₂ and reaching the receiver at any instant are out of phase (phase difference of π or 180°). They interfere destructively as shown in Figure 11.32. They will cancel each other.

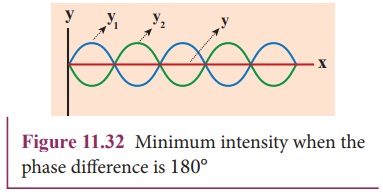
Therefore, the amplitude is minimum or zero amplitude which means no sound. No sound intensity is detected by the receiver in this case. The relation between path difference and phase difference is

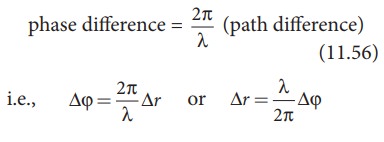
EXAMPLE 11.16

Consider two sources A and B as shown in the figure below. Let the two sources emit simple harmonic waves of same frequency but of different amplitudes, and both are in phase (same phase). Let O be any point equidistant from A and B as shown in the figure. Calculate the intensity at points O, Y and X. (X and Y’ are not equidistant from A & B)

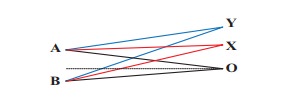
Solution

The distance between OA and OB are the same and hence, the waves starting from A and B reach O after covering equal distances (equal path lengths). Thus, the path difference between two waves at O is zero.

OA − OB = 0

Since the waves are in the same phase, at the point O, the phase difference between two waves is also zero. Thus, the resultant intensity at the point O is maximum.

Consider a point Y, such that the path difference between two waves is λ. Then the phase difference at Y is

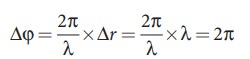
Therefore, at the point Y, the two waves from A and B are in phase, hence, the intensity will be maximum.

Consider a point X, and let the path difference the between two waves be λ/2.

Then the phase difference at X is

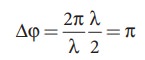
Therefore, at the point X, the waves meet and are in out of phase, Hence, due to destructive interference, the intensity will be minimum.

EXAMPLE 11.17

Two speakers C and E are placed 5 m apart and are driven by the same source. Let a man stand at A which is 10 m away from the mid point O of C and E. The man walks towards the point O which is at 1 m (parallel to OC) as shown in the figure. He receives the first minimum in sound intensity at B. Then calculate the frequency of the source.

(Assume speed of sound = 343 m s^-1)

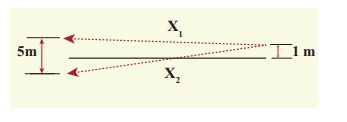
Solution

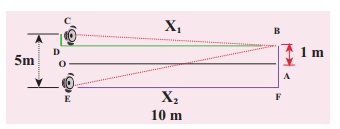
The first minimum occurs when the two waves reaching the point B are 180° (out of phase). The path difference ∆x = λ/2.

In order to calculate the path difference, we have to find the path lengths x₁ and x₂.

In a right triangle BDC,

The path difference ∆x = x₂ − x₁ = 10.6 m−10.1 m = 0.5 m. Required that this path difference

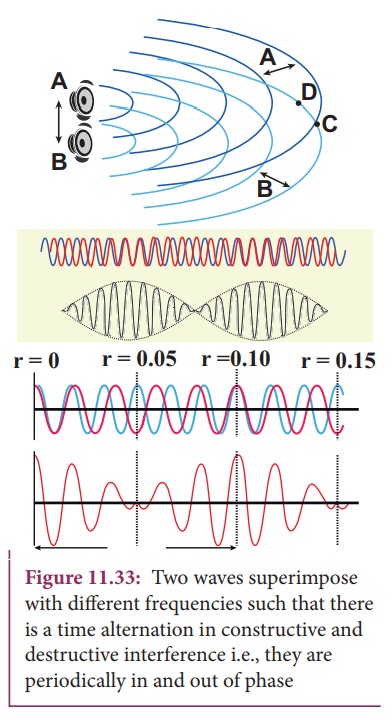
Formation of beats

When two or more waves superimpose each other with slightly different frequencies, then a sound of periodically varying amplitude at a point is observed. This phenomenon is known as beats. The number of amplitude maxima per second is called beat frequency. If we have two sources, then their difference in frequency gives the beat frequency.

Number of beats per second

n = | f₁ - f₂| per second

EXAMPLE 11.18

Consider two sound waves with wavelengths 5 m and 6 m. If these two waves propagate in a gas with velocity 330 ms-1. Calculate the number of beats per second.

Solution

Given λ₁ = 5m and λ₂ = 6m

Velocity of sound waves in a gas is v = 330 ms^-1

The relation between wavelength and velocity is v = λf => f = v/λ

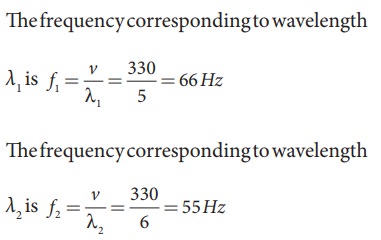
The number of beats per second is

| f₁ − f₂| = |66 − 55| = 11 beats per sec

EXAMPLE 11.19

Two vibrating tuning forks produce waves whose equation is given by y₁ = 5 sin(240π t) and y₂ = 4 sin(244πt). Compute the number of beats per second.

Solution

Given y₁ = 5 sin(240π t) and y₂ = 4 sin(244πt)

Comparing with y = A sin(2π f₁t), we get

2πf₁ = 240π ⇒ f₁ = 120Hz

2πf₂ = 244π ⇒ f₂ = 122Hz

The number of beats produced is | f₁ − f₂| = |120 − 122| = |− 2|=2 beats per sec