Chapter: 11th Physics : UNIT 11 : Waves
Velocity of longitudinal waves in an elastic medium
we shall derive the velocity of waves in two different cases:
1. The velocity of a transverse waves along a stretched string.
2. The velocity of a longitudinal waves in an elastic medium.
Velocity of longitudinal waves in an elastic medium
Consider an elastic medium (here we assume air) having a fixed mass contained in a long tube (cylinder) whose cross sectional area is A and maintained under a pressure P. One can generate longitudinal waves in the fluid either by displacing the fluid using a piston or by keeping a vibrating tuning fork at one end of the tube. Let us assume that the direction of propagation of waves coincides with the
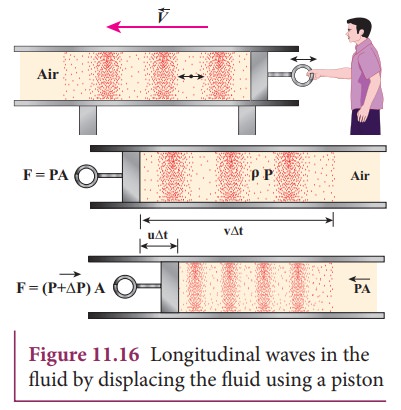
Let ρ be the density of the fluid which is initially at rest. At t = 0, the piston at left end of the tube is set in motion toward the right with a speed u.
Let u be the velocity of the piston and v be the velocity of the elastic wave. In time interval ∆t, the distance moved by the piston ∆d = u∆t. Now, the distance moved by the elastic disturbance is ∆x = v∆t. Let m be the mass of the air that has attained a velocity v in a time ∆t . Therefore,
m = ρ A∆x = ρ A (v∆t)
Then, the momentum imparted due to motion of piston with velocity u is
p = [ρ A (v t)]u
But the change in momentum is impulse.
The net impulse is
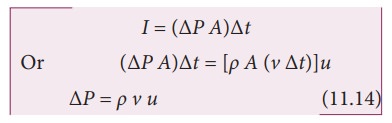
When the sound wave passes through air, the small volume element (ΔV) of the air undergoes regular compressions and rarefactions. So, the change in pressure can also be written as
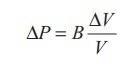
where, V is original volume and B is known as bulk modulus of the elastic medium.
But V = A ∆x = A v ∆t and
∆V = A ∆d =A u ∆t
Therefore,

Comparing equation (11.14) and equation (11.15), we get
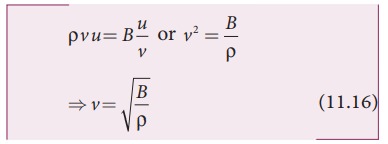
In general, the velocity of a longitudinal wave in elastic medium is v = √E/√P where E is the modulus of elasticity of the medium.
Cases: For a solid :
(i) one dimension rod (1D)

where Y is the Young’s modulus of the material of the rod and ρ is the density of the rod. The 1D rod will have only Young’s modulus.
(ii)Three dimension rod (3D) The speed of longitudinal wave in a solid is
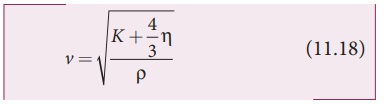
where η is the modulus of rigidity, K is the bulk modulus and ρ is the density of the rod.
Cases: For liquids:
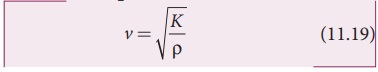
where, K is the bulk modulus and ρ is the density of the rod.
EXAMPLE 11.7
Calculate the speed of sound in a steel rod whose Young’s modulus Y = 2 × 1011 N m-2 and ρ = 7800 kg m-3.
Solution
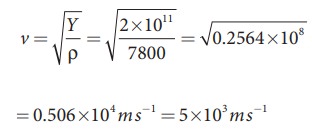
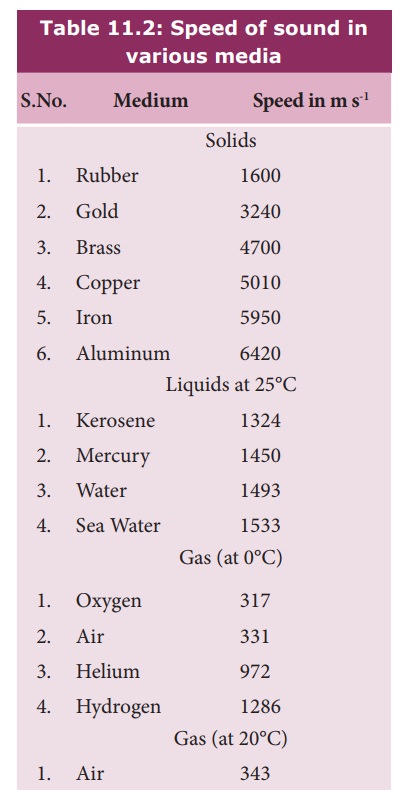
Therefore, longitudinal waves travel faster in a solid than in a liquid or a gas. Now you may understand why a shepherd checks before crossing railway track by keeping his ears on the rails to safegaurd his cattle.
EXAMPLE 11.8
An increase in pressure of 100 kPa causes a certain volume of water to decrease by 0.005% of its original volume.
(a) Calculate the bulk modulus of water?.
(b) Compute the speed of sound (compressional waves) in water?.
Solution
(a) Bulk modulus
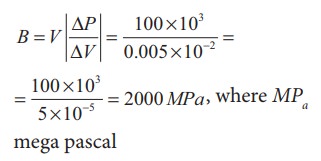
(b) Speed of sound in water is
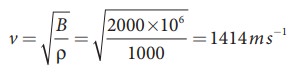
Related Topics