Chapter: 11th Physics : UNIT 11 : Waves
Solved Example Problems for Physics: Waves
Numerical Problems
1. The speed of a wave in a certain medium is 900 m/s. If 3000 waves passes over a certain point of the medium in 2 minutes, then compute its wavelength?.
Solution
The speed of a wave in
medium v = 900 ms-1
Freq. of wave = no. of
waves passing per sec (n) = 3000
waves/2min = 3000 / 2×60 = 25s
Wave length = λ =?
v
= n λ
λ = v/n
A = 900/25 =36m
A = 36m
Answer : λ = 36 m
2. Consider a mixture of 2 mol of helium and 4 mol of oxygen. Compute the speed of sound in this gas mixture at 300 K.
Solution
Helium - 2 mole, oxygen
- 4 mol
He & O2
are mixed, hence molecular weight of the mixture of gases

Answer : 400.9 ms-1
3. A ship in a sea sends SONAR waves straight down into the seawater from the bottom of the ship. The signal reflects from the deep bottom bed rock and returns to the ship after 3.5 s. After the ship moves to 100 km it sends another signal which returns back after 2s. Calculate the depth of the sea in each case and also compute the difference in height between two cases.
Solution
Velocity of SONAR waves
in water C = 1500 ms-1
Time taken by be wave
after reflection from the bottom of sea
2t = 3.5s
t =1.75s
Distance covered (d) =
?
C = d/t => d = c.t = 1500 × 1.75 - 2625 m
After moving 100km
The time taken by the
wave = 2t = 2s
T = 2/2 = 1s
d =?
d = 1500 × l
= 1500
The different between
these two heights . = 2625 - 1500
= 1125m
Answer : Δd = 1149.75 m
4. A sound wave is transmitted into a tube as shown in figure. The sound wave splits into two waves at the point A which recombine at point B. Let R be the radius of the semi-circle which is varied until the first minimum. Calculate the radius of the semi-circle if the wavelength of the sound is 50.0 m.
Answer : R = 21.9 m
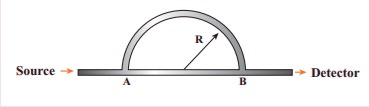
Solution
Consider the sound
waves start from the pt A. The sound waves will meet at the picture B &
interfere and can be detected.
The path length of
sound waves passing through the curve is equal to half the circle having radio
centered at c.
Thus, be path length of
be sound waves in curve part is
L1 = πγ
The path length of the
sound in tube ABC is equal to the diameter of the circle having radius γ
centered at e.
So the path length of
the sound waves travelling in it = L2 =2r
The path difference of
the sound waves at the picture is
ΔP = L1 - L2
= πr— 2r
ΔP = r(π - 2) ...(1)
For the sound to be
heard minimum at the detected the difference in path length of be sound waves
is
ΔP = λ/2 …………(2)
From equation (1)
r(π- 2) = λ/2
wavelength of sound = λ
= 50m
radius of be semicircle
r = ?
r = 50 / [2 × 3.14 – 4]
= 50/2.28
r = 21.9m
Answer : R = 21.9 m
5. N tuning forks are arranged in order of increasing frequency and any two successive tuning forks give n beats per second when sounded together. If the last fork gives double the frequency of the first (called as octave), Show that the frequency of the first tuning fork is f = (N−1)n.
Solution
No.of tuning forks = N
The frequency of the
first is double to be last
The difference of
frequency for two successive tuning forks NHz
Let be frequency of the
first tuning fork is f
Then be frequency of
the last tuning fork is f(N-l)n
frequency is reduced to
are fourth
flast
= - f /2
an = a + (n-1)d
(i.e.) 2f = f + (N-1)n
= (N-1)n
f
=
(N-1)n
6. Let the source propagate a sound wave whose intensity at a point (initially) be I. Suppose we consider a case when the amplitude of the sound wave is doubled and the frequency is reduced to one-fourth. Calculate now the new intensity of sound at the same point ?.
Solution
Intensity of sound
wave = Iold
Amplitude is doubled =
2A = Anew
Frequency is produced to are fourth
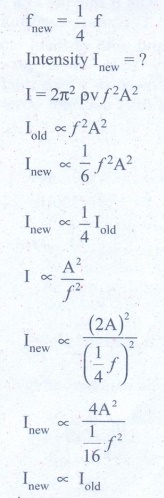
Answer: Inew ∝ ¼ I old
7. Consider two organ pipes of same length in which one organ pipe is closed and another organ pipe is open. If the fundamental frequency of closed pipe is 250 Hz. Calculate the fundamental frequency of the open pipe.

Answer: 500Hz
8. A police in a siren car moving with a velocity 20 ms-1 chases a thief who is moving in a car with a velocity v0ms-1. The police car sounds atfrequency 300Hz, and both of them move towards a stationary siren of frequency 400Hz. Calculate the speed in which thief is moving.
Solution
The velocity of car =
20ms-1
The frequency of car =
300Hz
The frequency
stationary siren = 400Hz
The speed in which
thief moving = ?

Answer: vthief = 10 m s-1
9. Consider the following function
(a) y = x2 + 2 α t x
(b) y = (x + vt)2
which among the above function can be characterized as a wave ?.
Solution
(a) y = x2 + 2 a t x
It is not describing
wave.
(b) y = (x + 2 vx)2
It satisfies wave
equation.
Answer: (a) function is not describing wave (b) satisfies wave equation.




Conceptual Questions
1. Why is it that transverse waves cannot be produced in a gas?. Can the transverse waves can be produced in solids and liquids?
Answer:
Transverse
waves travel in the form of crests and troughs and so involve change in shape.
As gas has no elasticity of shape, transverse waves cannot be produced in it.
2. Why is the roar of our national animal different from the sound of a mosquito?
Answer:
Roaring
of a national animal (tiger) produces a sound of low pitch and high intensity
or loudness, whereas the buzzing of mosquito produces a sound of high pitch and
low intensity or loudness.
3. A sound source and listener are both stationary and a strong wind is blowing. Is there a Doppler effect?
Answer: Yes. It does not
matter whether there is sound I source or transmission media in motion.
4. In an empty room why is it that a tone sounds louder than in the room having things like furniture etc.
Answer: Sound is a form of
energy. The furniture which act as obstacles absorbs most of the energy. So the
intensity of sound become low but in empty room, due to the absence of
obstacles the intensity of sound remain mostly same and we feel it louder.
5. How do animals sense impending danger of hurricane?
Answer: Some animals are
believed to be sensitive to low frequency sound waves emitted by hurricanes. They
can also detect the slight fall in air pressure, and water pressure that signal
a storm's approach.
6. Is it possible to realize whether a vessel kept under the tap is about to fill with water?
Answer:
The frequency of the note produced by an air column is inversely proportional
to its length. As the level of water in the vessel rises, the length of the air
column above it decreases. It produce, sound of decreasing frequency, i.e., the
sound becomes shorter. From the shrillness of sound, is possible to realize
whether the vessel is filled with water.
vmin
=
11.71 ms-1
Answer:
The frequency of the note produced by an air column is inversely proportional
to its length. As the level of water in the vessel rises, the length of the air
column above it decreases. It produce, sound of decreasing frequency, i.e., the
sound becomes shorter. From the shrillness of sound, is possible to realize
whether the vessel is filled with water.
vmin
=
11.71 ms-1
Solved Example Problems for Wave Motion
EXAMPLE 11.1
Which of the following has longer wavelength?
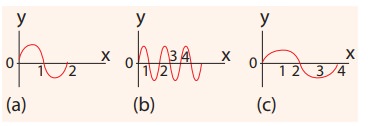
Answer is (c)
EXAMPLE 11.2
Three waves are shown in the figure below
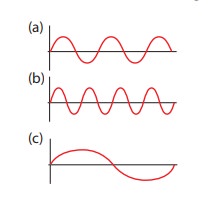
Write down
(a) the frequency in ascending order
(b) the wavelength in ascending order
Solution
(a) fc < fa < fb
(b) λb < λa < λc
From the example 11.2, we observe that the frequency is inversely related to the wavelength, f ∝ 1/λ
Then, fλ is equal to what?
[(i.e) fλ=?]
A simple dimensional argument will help us to determine this unknown physical quantity.
Dimension of wavelength is, [λ] = L
Frequency f = 1/ Time period , which implies that the dimension of frequency is,
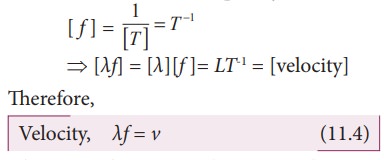
where v is known as the wave velocity or phase velocity. This is the velocity with which the wave propagates. Wave velocity is the distance travelled by a wave in one second.
Note:
1. The number of cycles (or revolutions) per unit time is called angular frequency. Angular frequency, ω = 2π/T = 2πf (unit is radians/second)
2. The number of cycles per unit distance or number of waves per unit distance is called wave number.
wave number, k = 2π/λ (unit is radians/ meter)
In two, three or higher dimensional case, the wave number is the magnitude of a vector called wave vector. The points in space of wave vectors are called reciprocal vectors, ![]() .
.
Dimensions of ![]() is L-1.
is L-1.
The velocity v, angular frequency ω and wave number λ are related as:
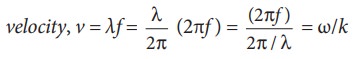
Wave numbers and wave vectors play an essential role in optics and scattering theory.
EXAMPLE 11.3
The average range of frequencies at which human beings can hear sound waves varies from 20 Hz to 20 kHz. Calculate the wavelength of the sound wave in these limits. (Assume the speed of sound to be 340 m s-1.
Solution
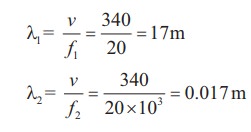
Therefore, the audible wavelength region is from 0.017 m to 17 m when the velocity of sound in that region is 340 m s-1.
EXAMPLE 11.4
A man saw a toy duck on a wave in an ocean. He noticed that the duck moved up and down 15 times per minute. He roughly measured the wavelength of the ocean wave as 1.2 m. Calculate the time taken by the toy duck for going one time up and down and also the velocity of the ocean wave.
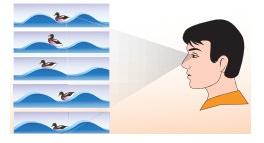
Solution
Given that the number of times the toy duck moves up and down is 15 times per minute. This information gives us frequency (the number of times the toy duck moves up and down)
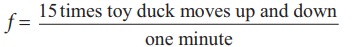
But one minute is 60 second, therefore, expressing time in terms of second
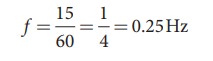
The time taken by the toy duck for going one time up and down is time period which is inverse of frequency
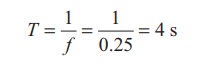
The velocity of ocean wave is v
v = λf = 1.2 ×0.25 = 0.3 m s-1.
EXAMPLE 11.5
Consider a string whose one end is attached to a wall. Then compute the following in both situations given in figure (assume waves crosses the distance in one second)
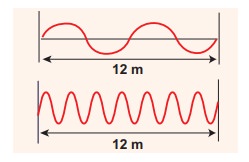
(a) Wavelength,
(b) Frequency and
(c) Velocity
Solution

This means that the speed of the wave along a string is a constant. Higher the frequency, shorter the wavelength and vice versa, and their product is velocity which remains the same.
Solved Example Problems for Velocity of Waves in Different Media
Velocity of transverse waves in a stretched string
EXAMPLE 11.6
Calculate the velocity of the travelling pulse as shown in the figure below. The linear mass density of pulse is 0.25 kg m-1. Further, compute the time taken by the travelling pulse to cover a distance of 30 cm on the string.
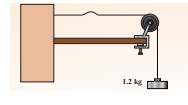
Solution
The tension in the string is T = m g = 1.2 × 9.8 = 11.76 N
The mass per unit length is μ = 0.25 kg m-1. Therefore, velocity of the wave pulse is
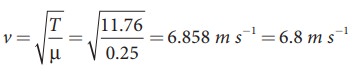
The time taken by the pulse to cover the distance of 30 cm is
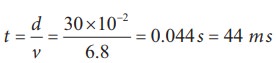
where
ms = milli second.
Velocity of longitudinal waves in an elastic medium
EXAMPLE 11.7
Calculate the speed of sound in a steel rod whose Young’s modulus Y = 2 × 1011 N m-2 and ρ = 7800 kg m-3.
Solution
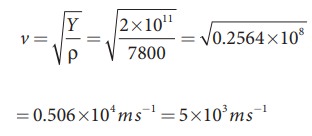
Therefore, longitudinal waves travel faster in a solid than in a liquid or a gas. Now you may understand why a shepherd checks before crossing railway track by keeping his ears on the rails to safegaurd his cattle.
EXAMPLE 11.8
An increase in pressure of 100 kPa causes a certain volume of water to decrease by 0.005% of its original volume.
(a) Calculate the bulk modulus of water?.
(b) Compute the speed of sound (compressional waves) in water?.
Solution
(a) Bulk modulus
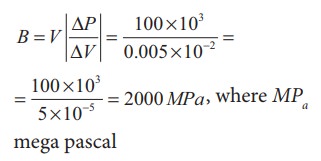
(b) Speed of sound in water is
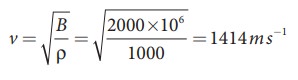
Solved Example Problems for Propagation of Sound Waves
EXAMPLE 11.9
The ratio of the densities of oxygen and nitrogen is 16:14. Calculate the temperature when the speed of sound in nitrogen gas at 17°C is equal to the speed of sound in oxygen gas.
Solution
From equation (11.25), we have

Where, R is the universal gas constant and M is the molecular mass of the gas. The speed of sound in nitrogen gas at 17°C is
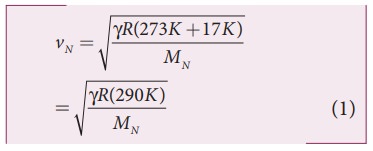
Similarly, the speed of sound in oxygen gas at t in K is
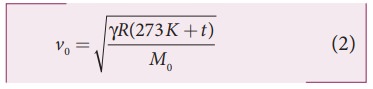
Given that the value of γ is same for both the gases, the two speeds must be equal. Hence, equating equation (1) and (2), we get
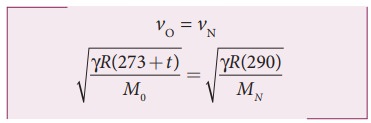
Squaring on both sides and cancelling γ R term and rearranging, we get
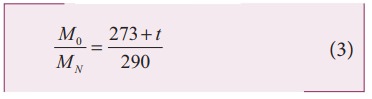
Since the densities of oxygen and nitrogen is 16:14,
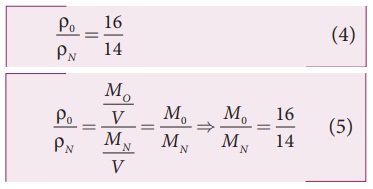
Substituting equation (5) in equation (3), we get

Solved Example Problems for Reflection of Sound Waves
EXAMPLE 11.10
Suppose a man stands at a distance from a cliff and claps his hands. He receives an echo from the cliff after 4 second. Calculate the distance between the man and the cliff. Assume the speed of sound to be 343 m s-1.
Solution
The time taken by the sound to come back as echo is 2t = 4 ⇒ t = 2 s
∴The distance is d = vt =(343 m s-1)(2 s) = 686 m.
Solved Example Problems for Progressive Waves (or) Travelling Waves
EXAMPLE 11.11
Sketch y = x −a for different values of a.
Solution
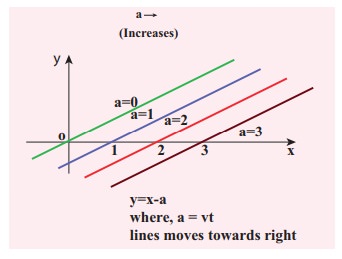
This implies, when increasing the value of a, the line shifts towards right side. For a = vt, y = x − vt satisfies the differential equation. Though this function satisfies the differential equation, it is not finite for all values of x and t. Hence, it does not represent a wave.
EXAMPLE 11.12
How does the wave y = sin(x − a) for a = 0, a = π/4, a = π/2, a = 3π/2, a = π look like?. Sketch this wave.
Solution
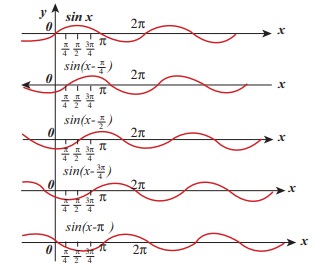
From the above picture we observe that y = sin (x−a) for a = 0, a = π/4, a = π/2, a = 3π/2 and a = π, the function y = sin (x−a) shifts towards right. Further, we can take a = vt and v = π/4 , and sketching for different times t = 0s, t = 1 s, t = 2s etc., we once again observe that y = sin(x−vt) moves towards the right. Hence, y = sin(x−vt) is a travelling (or progressive) wave moving towards the right. If y = sin(x+vt) then the travelling (or progressive) wave moves towards the left. Thus, any arbitrary function of type y = f(x−vt) characterising the wave must move towards right and similarly, any arbitrary function of type y = f(x+vt) characterizing the wave must move towards left.
EXAMPLE 11.13
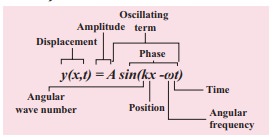
Check the dimensional of the wave y = sin(x−vt). If it is dimensionally wrong, write the above equation in the correct form.
Solution
Dimensionally it is not correct. we know that y = sin(x−vt) must be a dimensionless quantity but x−vt has dimension. The correct equation is y = sin (k x−ωt), where k and ω have the dimensions of inverse of length and inverse of time respectively. The sine functions and cosine functions are periodic functions with period 2π. Therefore, the correct expression is y = sin ([2π/λ]x, [2π/T]t) where λ and T are wavelength and time period, respectively.
In general, y(x,t)=A sin(k x−ωt).
EXAMPLE 11.14
The wavelength of two sine waves are λ1 = 1m and λ2 = 6m. Calculate the corresponding wave numbers.
Solution
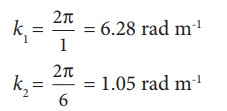
EXAMPLE 11.15
A mobile phone tower transmits a wave signal of frequency 900MHz. Calculate the length of the waves transmitted from the mobile phone tower.
Solution
Frequency, f = 900 MHz = 900 ×106 Hz
The speed of wave is c = 3 × 108m s−1
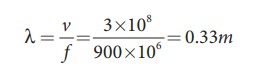
Solved Example Problems for Waves Superposition Principle
Interference of waves
EXAMPLE 11.16
Consider two sources A and B as shown in the figure below. Let the two sources emit simple harmonic waves of same frequency but of different amplitudes, and both are in phase (same phase). Let O be any point equidistant from A and B as shown in the figure. Calculate the intensity at points O, Y and X. (X and Y’ are not equidistant from A & B)
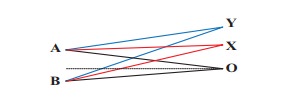
Solution
The distance between OA and OB are the same and hence, the waves starting from A and B reach O after covering equal distances (equal path lengths). Thus, the path difference between two waves at O is zero.
OA − OB = 0
Since the waves are in the same phase, at the point O, the phase difference between two waves is also zero. Thus, the resultant intensity at the point O is maximum.
Consider a point Y, such that the path difference between two waves is λ. Then the phase difference at Y is
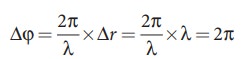
Therefore, at the point Y, the two waves from A and B are in phase, hence, the intensity will be maximum.
Consider a point X, and let the path difference the between two waves be λ/2.
Then the phase difference at X is
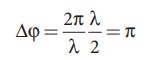
Therefore, at the point X, the waves meet and are in out of phase, Hence, due to destructive interference, the intensity will be minimum.
EXAMPLE 11.17
Two speakers C and E are placed 5 m apart and are driven by the same source. Let a man stand at A which is 10 m away from the mid point O of C and E. The man walks towards the point O which is at 1 m (parallel to OC) as shown in the figure. He receives the first minimum in sound intensity at B. Then calculate the frequency of the source.
(Assume speed of sound = 343 m s-1)
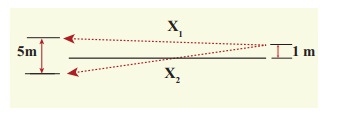
Solution
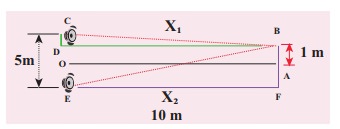
The first minimum occurs when the two waves reaching the point B are 180° (out of phase). The path difference ∆x = λ/2.
In order to calculate the path difference, we have to find the path lengths x1 and x2.
In a right triangle BDC,

The path difference ∆x = x2 − x1 = 10.6 m−10.1 m = 0.5 m. Required that this path difference

Formation of beats
EXAMPLE 11.18
Consider two sound waves with wavelengths 5 m and 6 m. If these two waves propagate in a gas with velocity 330 ms-1. Calculate the number of beats per second.
Solution
Given λ1 = 5m and λ2 = 6m
Velocity of sound waves in a gas is v = 330 ms-1
The relation between wavelength and velocity is v = λf => f = v/λ
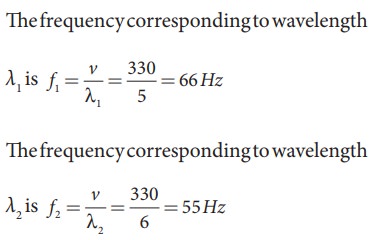
The number of beats per second is
| f1 − f2| = |66 − 55| = 11 beats per sec
EXAMPLE 11.19
Two vibrating tuning forks produce waves whose equation is given by y1 = 5 sin(240π t) and y2 = 4 sin(244πt). Compute the number of beats per second.
Solution
Given y1 = 5 sin(240π t) and y2 = 4 sin(244πt)
Comparing with y = A sin(2π f1t), we get
2πf1 = 240π ⇒ f1 = 120Hz
2πf2 = 244π ⇒ f2 = 122Hz
The number of beats produced is | f1 − f2| = |120 − 122| = |− 2|=2 beats per sec
Solved Example Problems for Stationary waves
EXAMPLE 11.20
Compute the distance between anti-node and neighbouring node.
Solution
For nth mode, the distance between anti-node and neighbouring node is
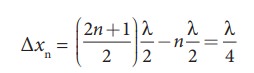
EXAMPLE 11.21
Let f be the fundamental frequency of the string. If the string is divided into three segments l1, l2 and l3 such that the fundamental frequencies of each segments be f1, f2 and f3, respectively. Show that
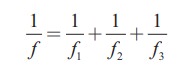
Solution
For a fixed tension T and mass density µ, frequency is inversely proportional to the string length i.e.
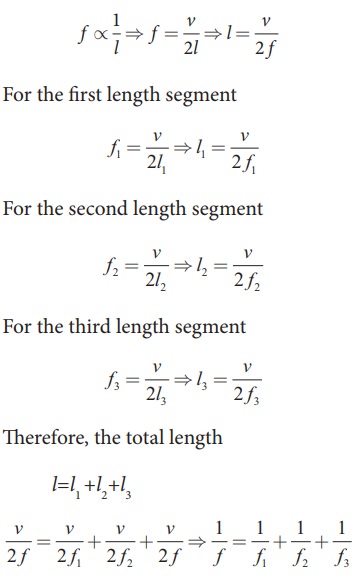
EXAMPLE 11.22
Consider a string in a guitar whose length is 80 cm and a mass of 0.32 g with tension 80 N is plucked. Compute the first four lowest frequencies produced when it is plucked.
Solution
The velocity of the wave
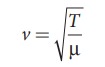
The length of the string, L = 80 cm=0.8 m The mass of the string, m = 0.32 g = 0.32 × 10-3kg
Therefore, the linear mass density,
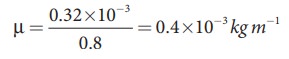
The tension in the string, T = 80 N
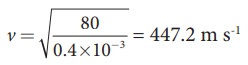
The wavelength corresponding to the fundamental frequency f1 is λ1 = 2L = 2 × 0.8 = 1.6 m
The fundamental frequency f1 corresponding to the wavelength λ1
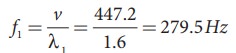
Similarly, the frequency corresponding to the second harmonics, third harmonics and fourth harmonics are
f2 = 2f1 = 559 Hz
f3 = 3f1 = 838.5 Hz
f4 = 4f1 = 1118 Hz
Solved Example Problems for Intensity and Loudness of sound
EXAMPLE 11.23
A baby cries on seeing a dog and the cry is detected at a distance of 3.0 m such that the intensity of sound at this distance is 10-2 W m-2. Calculate the intensity of the baby’s cry at a distance 6.0 m.
Solution
I1 is the intensity of sound detected at a distance 3.0 m and it is given as 10-2 W m-2. Let I2 be the intensity of sound detected at a distance 6.0 m. Then,
r1 = 3.0 m,
r2 = 6.0 m
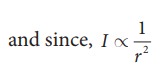
the power output does not depend on the observer and depends on the baby. Therefore,
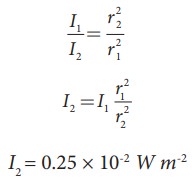
I2 = 0.25 × 10-2 W m-2
EXAMPLE 11.24
The sound level from a musical instrument playing is 50 dB. If three identical musical instruments are played together then compute the total intensity. The intensity of the sound from each instrument is 10-12 Wm-2
Solution
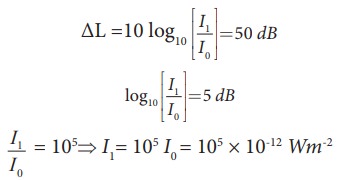
I1 = 10-7 Wm-2
Since three musical instruments are played, therefore, Itotal = 3I1 = 3 × 10-7 Wm-2.
Solved Example Problems for Vibrations of Air Column
EXAMPLE 11.25
If a flute sounds a note with 450Hz , what are the frequencies of the second, third, and fourth harmonics of this pitch?. If the clarinet sounds with a same note as 450Hz, then what are the frequencies of the lowest three harmonics produced ?.
Solution
For a flute which is an open pipe, we have
Second harmonics f2 = 2 f1 = 900 Hz
Third harmonics f3 = 3 f1 = 1350 Hz
Fourth harmonics f4 = 4 f1 = 1800 Hz
For a clarinet which is a closed pipe, we have
Second harmonics f 2 = 3 f1 = 1350 Hz
Third harmonics f 3 = 5 f1 = 2250 Hz
Fourth harmonics f 4 = 7 f1 = 3150 Hz
EXAMPLE 11.26
If the third harmonics of a closed organ pipe is equal to the fundamental frequency of an open organ pipe, compute the length of the open organ pipe if the length of the closed organ pipe is 30 cm.
Solution
Let l2 be the length of the open organ pipe, with l1 =30 cm the length of the closed organ pipe.
It is given that the third harmonic of closed organ pipe is equal to the fundamental frequency of open organ pipe.
The third harmonic of a closed organ pipe is
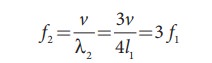
The fundamental frequency of open organ pipe is
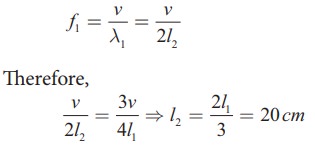
EXAMPLE 11.27
A frequency generator with fixed frequency of 343 Hz is allowed to vibrate above a 1.0 m high tube. A pump is switched on to fill the water slowly in the tube. In order to get resonance, what must be the minimum height of the water?. (speed of sound in air is 343 m s−1)
Solution
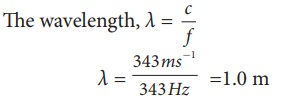
Let the length of the resonant columns be L1, L2 and L3. The first resonance occurs at length L1
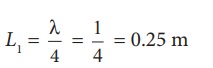
The second resonance occurs at length L2
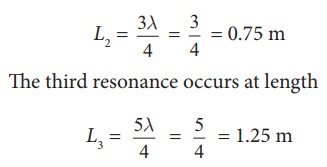
and so on.
Since total length of the tube is 1.0 m the third and other higher resonances do not occur. Therefore, the minimum height of water Hmin for resonance is,
Hmin = 1.0 m − 0.75 m = 0.25 m
EXAMPLE 11.28
A student performed an experiment to determine the speed of sound in air using the resonance column method. The length of the air column that resonates in the fundamental mode with a tuning fork is 0.2 m. If the length is varied such that the same tuning fork resonates with the first overtone at 0.7 m. Calculate the end correction.
Solution
End correction
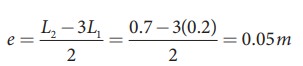
EXAMPLE 11.29
Consider a tuning fork which is used to produce resonance in an air column. A resonance air column is a glass tube whose length can be adjusted by a variable piston. At room temperature, the two successive resonances observed are at 20 cm and 85 cm of the column length. If the frequency of the length is 256 Hz, compute the velocity of the sound in air at room temperature.
Solution
Given two successive length (resonance) to be L1 = 20 cm and L2 = 85 cm
The frequency is f = 256 Hz
v = f λ = 2f∆L = 2f (L2 − L1)
= 2 × 256 × (85 − 20) × 10−2 m s−1
v= 332.8 cm−1
Solved Example Problems for Doppler Effect
EXAMPLE 11.30
A sound of frequency 1500 Hz is emitted by a source which moves away from an observer and moves towards a cliff at a speed of 6 ms-1.
(a) Calculate the frequency of the sound which is coming directly from the source.
(b) Compute the frequency of sound heard by the observer reflected off the cliff. Assume the speed of sound in air is 330 m s-1
Solution
(a) Source is moving away and observer is stationary, therefore, the frequency of sound heard directly from source is
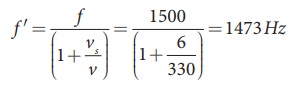
(b) Sound is reflected from the cliff and reaches observer, therefore,
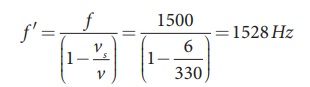
EXAMPLE 11.31
An observer observes two moving trains, one reaching the station and other leaving the station with equal speeds of 8 m s−1. If each train sounds its whistles with frequency 240 Hz, then calculate the number of beats heard by the observer.
Solution:
Observer is stationary
(i) Source (train) is moving towards an observer:
Apparent frequency due to train arriving station is
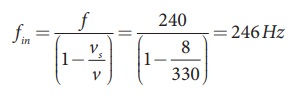
(ii) Source (train) is moving away form an observer:
Apparent frequency due to train leaving station is
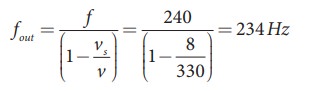
So the number of beats = | fin -fout| = (246-234) = 12
Related Topics