Resonance air column apparatus

Resonance air column apparatus

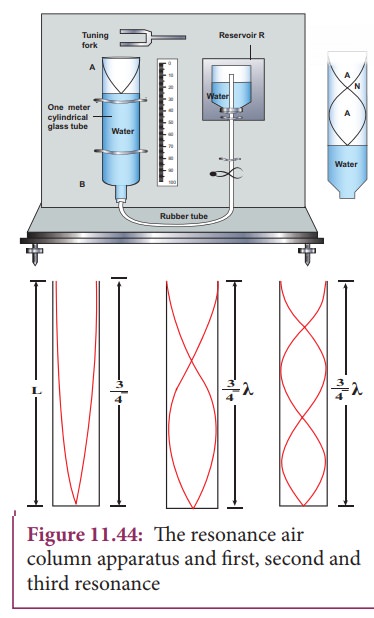
The resonance air column apparatus is one of the simplest techniques to measure the speed of sound in air at room temperature. It consists of a cylindrical glass tube of one meter length whose one end A is open and another end B is connected to the water reservoir R through a rubber tube as shown in Figure 11.44. This cylindrical glass tube is mounted on a vertical stand with a scale attached to it. The tube is partially filled with water and the water level can be adjusted by raising or lowering the water in the reservoir R. The surface of the water will act as a closed end and other as the open end. Therefore, it behaves like a closed organ pipe, forming nodes at the surface of water and antinodes at the closed end. When a vibrating tuning fork is brought near the open end of the tube, longitudinal waves are formed inside the air column. These waves move downward as shown in Figure 11.44, and reach the surfaces of water and get reflected and produce standing waves. The length of the air column is varied by changing the water level until a loud sound is produced in the air column. At this particular length the frequency of waves in the air column resonates with the frequency of the tuning fork (natural frequency of the tuning fork). At resonance, the frequency of sound waves produced is equal to the frequency of the tuning fork. This will occur only when the length of air column is proportional to (1/4)^th of the  wavelength of the sound waves produced.

Let the first resonance occur at length L₁, then

But since the antinodes are not exactly formed at the open end, we have to include a correction, called end correction e, by assuming that the antinode is formed at some small distance above the open end. Including this end correction, the first resonance is

Now the length of the air column is increased to get the second resonance. Let L₂ be the length at which the second resonance occurs. Again taking end correction into account, we have

In order to avoid end correction, let us take the difference of equation (11.80) and equation (11.79), we get

The speed of the sound in air at room temperature can be computed by using the formula

v = f λ = 2f∆L

Further, to compute the end correction, we use equation (11.81) and equation (11.82), we get

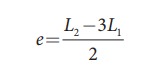
EXAMPLE 11.27

A frequency generator with fixed frequency of 343 Hz is allowed to vibrate above a 1.0 m high tube. A pump is switched on to fill the water slowly in the tube. In order to get resonance, what must be the minimum height of the water?. (speed of sound in air is 343 m s^−1)

Solution

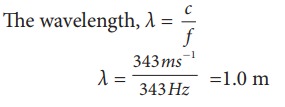
Let the length of the resonant columns be L₁, L₂ and L₃. The first resonance occurs at length L₁

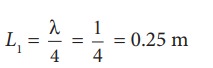
The second resonance occurs at length L₂

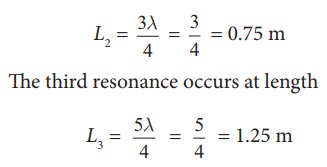
and so on.

Since total length of the tube is 1.0 m the third and other higher resonances do not occur. Therefore, the minimum height of water H_min for resonance is,

H_min = 1.0 m − 0.75 m = 0.25 m

EXAMPLE 11.28

A student performed an experiment to determine the speed of sound in air using the resonance column method. The length of the air column that resonates in the fundamental mode with a tuning fork is 0.2 m. If the length is varied such that the same tuning fork resonates with the first overtone at 0.7 m. Calculate the end correction.

Solution

End correction

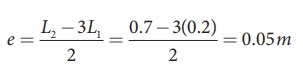
EXAMPLE 11.29

Consider a tuning fork which is used to produce resonance in an air column. A resonance air column is a glass tube whose length can be adjusted by a variable piston. At room temperature, the two successive resonances observed are at 20 cm and 85 cm of the column length. If the frequency of the length is 256 Hz, compute the velocity of the sound in air at room temperature.

Solution

Given two successive length (resonance) to be L₁ = 20 cm and L₂ = 85 cm

The frequency is f = 256 Hz

v = f λ = 2f∆L = 2f (L₂ − L₁)

= 2 × 256 × (85 − 20) × 10^−2 m s^−1

v= 332.8 cm^−1