Newton’s formula for speed of sound waves in air

Newton’s formula for speed of sound waves in air

Sir Isaac Newton assumed that when sound propagates in air, the formation of compression and rarefaction takes place in a very slow manner so that the process is isothermal in nature. That is, the heat produced during compression (pressure increases, volume decreases), and heat lost during rarefaction (pressure decreases, volume increases) occur over a period of time such that the temperature of the medium remains constant. Therefore, by treating the air molecules to form an ideal gas, the changes in pressure and volume obey Boyle’s law, Mathematically

Differentiating equation (11.20), we get

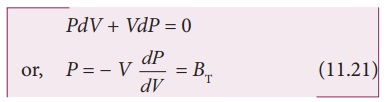
where, BT is an isothermal bulk modulus of air. Substituting equation (11.21) in equation (11.16), the speed of sound in air is

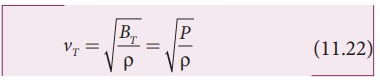
Since P is the pressure of air whose value at NTP (Normal Temperature and Pressure) is 76 cm of mercury, we have

P = (0.76 × 13.6 ×103 × 9.8) N m-2

ρ= 1.293 kg m-3. here ρ is density of air

Then the speed of sound in air at Normal Temperature and Pressure (NTP) is

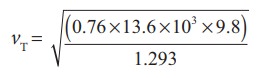
=279.80 m s-1 ≈ 280 ms-1 (theoretical value)

But the speed of sound in air at 0°C is experimentally observed as 332 m s-1 which is close upto 16% more than theoretical value (Percentage error is ([332-280]/332 x 100% = 15.6%).

This error is not small