Stationary waves in sonometer: Construction, Working and Example Problem

Stationary waves in sonometer

Sono means sound related, and sonometer implies sound-related measurements. It is a device for demonstrating the relationship between the frequency of the sound produced in the transverse standing wave in a string, and the tension, length and mass per unit length of the string. Therefore, using this device, we can determine the following quantities:

(a) the frequency of the tuning fork or frequency of alternating current

(b) the tension in the string

(c) the unknown hanging mass

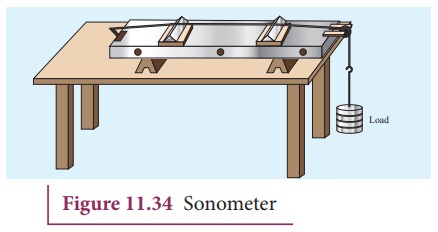
Construction:

The sonometer is made up of a hollow box which is one meter long with a uniform metallic thin string attached to it. One end of the string is connected to a hook and the other end is connected to a weight hanger through a pulley as shown in Figure 11.34. Since only one string is used, it is also known as monochord. The weights are added to the free end of the wire to increase the tension of the wire. Two adjustable wooden knives are put over the board, and their positions are adjusted to change the vibrating length of the stretched wire.

Working :

A transverse stationary or standing wave is produced and hence, at the knife edges P and Q, nodes are formed. In between the knife edges, anti-nodes are formed.

If the length of the vibrating element is l then

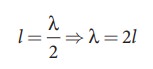
Let f be the frequency of the vibrating element, T the tension of in the string and μ the mass per unit length of the string. Then using equation (11.13), we get

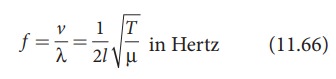
Let ρ be the density of the material of the string and d be the diameter of the string. Then the mass per unit length μ,

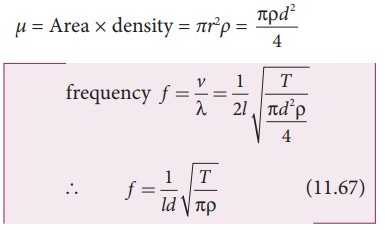
EXAMPLE 11.21

Let f be the fundamental frequency of the string. If the string is divided into three segments l1, l2 and l3 such that the fundamental frequencies of each segments be f1, f2 and f3, respectively. Show that

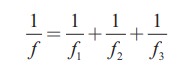
Solution

For a fixed tension T and mass density µ, frequency is inversely proportional to the string length i.e.