Chapter: 11th Physics : UNIT 11 : Waves
Propagation of Sound Waves
PROPAGATION
OF SOUND WAVES
We
know that sound waves are longitudinal waves, and when they propagate
compressions and rarefactions are formed. In the following section, we compute
the speed of sound in air by Newton’s method and also discuss the Laplace
correction and the factors affecting sound in air.
Newton’s formula for speed of sound waves in air
Sir
Isaac Newton assumed that when sound propagates in air, the formation of
compression and rarefaction takes place in a very slow manner so that the
process is isothermal in nature. That is, the heat produced during compression
(pressure increases, volume decreases), and heat lost during rarefaction
(pressure decreases, volume increases) occur over a period of time such that
the temperature of the medium remains constant. Therefore, by treating the air
molecules to form an ideal gas, the changes in pressure and volume obey Boyle’s
law, Mathematically

Differentiating
equation (11.20), we get
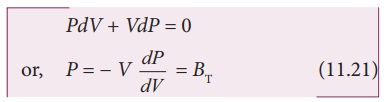
where,
BT is an isothermal bulk
modulus of air. Substituting equation (11.21) in equation (11.16), the speed of
sound in air is
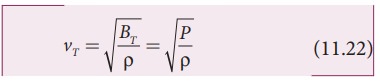
Since
P is the pressure of air whose value
at NTP (Normal Temperature and Pressure) is 76 cm of mercury, we have
![]()
![]() P = (0.76 × 13.6 ×103 × 9.8) N m-2
P = (0.76 × 13.6 ×103 × 9.8) N m-2
ρ=
1.293 kg m-3. here ρ is density of air
Then
the speed of sound in air at Normal Temperature and Pressure (NTP) is
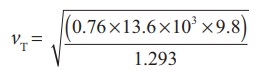
=279.80
m s-1 ≈ 280 ms-1 (theoretical value)
But
the speed of sound in air at 0°C is experimentally observed as 332 m s-1 which
is close upto 16% more than theoretical value (Percentage error is
([332-280]/332 x 100% = 15.6%).
This
error is not small
Laplace’s correction
In
1816, Laplace satisfactorily corrected this discrepancy by assuming that when
the sound propagates through a medium, the particles oscillate very rapidly
such that the compression and rarefaction occur very fast. Hence the exchange
of heat produced due to compression and cooling effect due to rarefaction do
not take place, because, air (medium) is a bad conductor of heat. Since,
temperature is no longer considered as a constant here, sound propagation is an
adiabatic process. By adiabatic considerations, the gas obeys Poisson’s law
(not Boyle’s law as Newton assumed), which is

which
is the ratio between specific heat at constant pressure and specific heat at
constant volume.
Differentiating
equation (11.23) on both the sides, we get
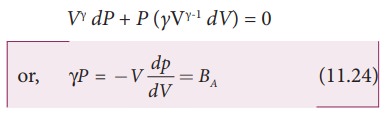
where,
BA is the adiabatic bulk
modulus of air. Now, substituting equation (11.24) in equation (11.16), the
speed of sound in air is
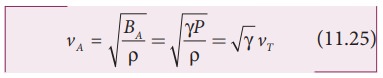
Since
air contains mainly, nitrogen, oxygen, hydrogen etc, (diatomic gas), we take γ=
1.47. Hence, speed of sound in air is vA = ( √1.4)(280 m s-1)= 331.30
m s-1, which is very much
closer to experimental data.
Factors affecting speed of sound in gases
Let
us consider an ideal gas whose equation of state is

where,
P is pressure, V is volume, T is temperature, n is number of mole and R is
universal gas constant. For a given mass of a molecule, equation (11.26) can be
written as

For
a fixed mass m, density of the gas inversely varies with volume. i.e.,
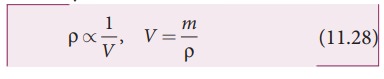
Substituting
equation (11.28) in equation (11.27), we get

where
c is constant.
The
speed of sound in air given in equation (11.25) can be written as
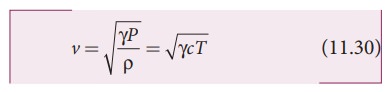
From
the above relation we observe the following
(a) Effect of pressure :
For
a fixed temperature, when the pressure varies, correspondingly density also
varies such that the ratio (P/ρ) becomes constant.
This
means that the speed of sound is independent of pressure for a fixed temperature.
If the temperature remains same at the top and the bottom of a mountain then
the speed of sound will remain same at these two points. But, in practice, the
temperatures are not same at top and bottom of a mountain; hence, the speed of
sound is different at different points.
(b) Effect of temperature :
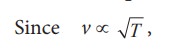
the
speed of sound varies directly to the square root of temperature in kelvin.
Let
v0 be the speed of sound
at temperature at 0° C or 273 K and v
be the speed of sound at any arbitrary temperature T (in kelvin), then
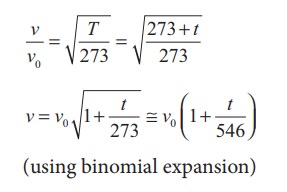
Since v0
= 331m s-1 at 00C,
v at any temperature in t0C is
v = (331 + 0.60t) m s-1
Thus
the speed of sound in air increases by 0.61 m s-1
per degree celcius rise in temperature. Note that when the temperature is
increased, the molecules will vibrate faster due to gain in thermal energy and
hence, speed of sound increases.
(c) Effect of density :
Let
us consider two gases with different densities having same temperature and
pressure. Then the speed of sound in the two gases are

Taking
ratio of equation (11.31) and equation (11.32), we get
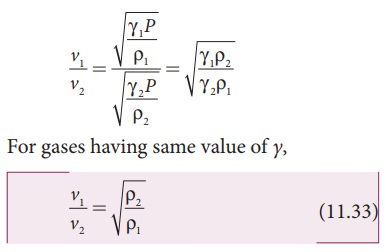
Thus
the velocity of sound in a gas is inversely proportional to the square root of
the density of the gas.
(d) Effect of moisture (humidity):
We
know that density of moist air is 0.625 of that of dry air, which means the
presence of moisture in air (increase in humidity) decreases its density.
Therefore, speed of sound increases with rise in humidity. From equation
(11.30)
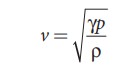
Let
ρ1, v1 and ρ2,
v2 be the density and
speeds of sound in dry air and moist air, respectively. Then
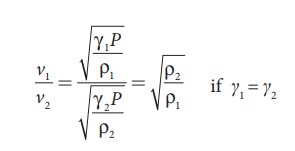
Since
P is the total atmospheric pressure,
it can be shown that
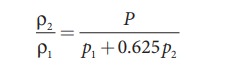
where
p1 and p2 are the partial pressures
of dry air and water vapour respectively. Then
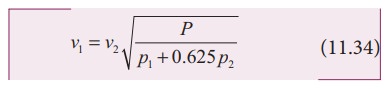
(e) Effect of wind:
The
speed of sound is also affected by blowing of wind. In the direction along the
wind blowing, the speed of sound increases whereas in the direction opposite to
wind blowing, the speed of sound decreases.
EXAMPLE 11.9
The
ratio of the densities of oxygen and nitrogen is 16:14. Calculate the
temperature when the speed of sound in nitrogen gas at 17°C is equal to the
speed of sound in oxygen gas.
Solution
From
equation (11.25), we have

Where,
R is the universal gas constant and M is the molecular mass of the gas. The
speed of sound in nitrogen gas at 17°C is
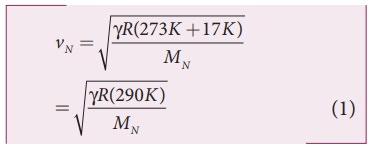
Similarly,
the speed of sound in oxygen gas at t
in K is
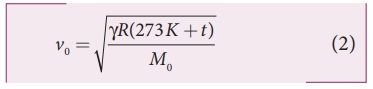
Given
that the value of γ is same for both
the gases, the two speeds must be equal. Hence, equating equation (1) and (2),
we get
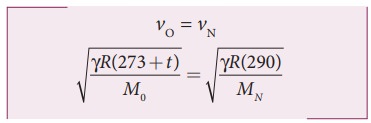
Squaring
on both sides and cancelling γ R term
and rearranging, we get

Since
the densities of oxygen and nitrogen is 16:14,

Substituting
equation (5) in equation (3), we get

Related Topics